Solenoid

Let 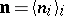be a sequence of positive integers. From 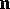one constructs a topological space as follows.

Let 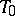be a torus in 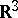; inside one takes a torus 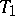wrapped around longitudinally 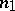times, in a smooth fashion without folding back; inside one takes a torus 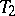wrapped around 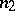times in the same way. Continuing this procedure indefinitely, one obtains a decreasing sequence of tori. Its intersection is called the 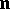-adic solenoid .

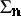The basic properties of 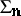are that it is a one-dimensional continuum which, moreover, is indecomposable (cf. Indecomposable continuum).

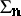is also a topological group; this can be seen if one considers an alternative construction of 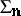as the inverse limit of the following inverse sequence:

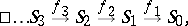where each 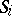is the unit circle and 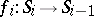is defined by 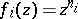. There are various other ways in which one can construct the solenoids, see, e.g., [a3].

Solenoids were first defined by L. Vietoris [a2] (for the sequence 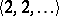) and by D. van Dantzig [a1] (for all constant sequences).

Solenoids are also important in topological dynamics; on them one can define a flow (continuous-time dynamical system) structure [a4] which has a locally disconnected minimal set of almost-periodic motions.

There is a complete classification of the solenoids: first, without loss of generality one may assume that the numbers 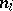are prime. Call two sequences of primes 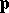and 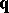equivalent if one can delete from each a finite number of terms such that in the reduced sequences 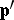and 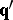every prime is counted the same number of times. One can then show that and 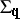are homeomorphic if and only if and are equivalent. See [a5] and [a6].

Finally one can characterize the solenoids as those metric continua that are homogeneous and have the property that every proper subcontinuum is an Arc (topology). See [a7].

References

[a1]	D. van Dantzig, "Ueber topologisch homogene Kontinua" Fund. Math. , 15 (1930) pp. 102–125
[a2]	L. Vietoris, "Über den höheren Zusammenhang kompakter Räume und eine Klasse von zusammenhangstreuen Abbildungen" Math. Ann. , 97 (1927) pp. 454–472
[a3]	E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1 , Springer (1979)
[a4]	V.V. Nemytskii, V.V. Stepanov, "Qualitative theory of differential equations" , Princeton Univ. Press (1960) (Translated from Russian)
[a5]	R.H. Bing, "A simple closed curve is the only homogeneous bounded plane continuum that contains an arc" Canad. Math. J. , 12 (1960) pp. 209–230
[a6]	M.C. McCord, "Inverse limit sequences with covering maps" Trans. Amer. Math. Soc. , 114 (1965) pp. 197–209
[a7]	C.L. Hagopian, "A characterization of solenoids" Pacific J. Math. , 68 (1977) pp. 425–435