Difference between revisions of "Wald identity"
(Importing text file) |
(→References: Feller: internal link) |
||
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A. Wald, "Sequential analysis", Wiley (1952)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''1''', Wiley (1957) pp. Chapt.14</TD></TR></table> |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 11:22, 4 May 2012
An identity in sequential analysis which states that the mathematical expectation of the sum  of a random number
of a random number  of independent, identically-distributed random variables
of independent, identically-distributed random variables  is equal to the product of the mathematical expectations
is equal to the product of the mathematical expectations  and
and  :
:
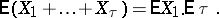 |
A sufficient condition for the Wald identity to be valid is that the mathematical expectations  and
and  in fact exist, and for the random variable
in fact exist, and for the random variable  to be a Markov time (i.e. for any
to be a Markov time (i.e. for any 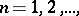 the event
the event 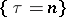 is determined by the values of the random variables
is determined by the values of the random variables 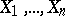 or, which is the same thing, the event
or, which is the same thing, the event 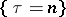 belongs to the
belongs to the 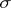 -algebra generated by the random variables
-algebra generated by the random variables  ). Wald's identity is a particular case of a fundamental theorem in sequential analysis stating that
). Wald's identity is a particular case of a fundamental theorem in sequential analysis stating that
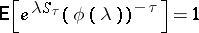 | (*) |
for all complex 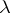 for which
for which 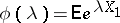 exists and
exists and  . It was established by A. Wald [1].
. It was established by A. Wald [1].
References
| [1] | A. Wald, "Sequential analysis", Wiley (1952) |
| [2] | W. Feller, "An introduction to probability theory and its applications", 1, Wiley (1957) pp. Chapt.14 |
Comments
The general result (*) is (also) referred to as Wald's formula.
References
| [a1] | A.V. [A.V. Skorokhod] Skorohod, "Random processes with independent increments" , Kluwer (1991) pp. 23 (Translated from Russian) |
Wald identity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wald_identity&oldid=25963