Difference between revisions of "Fourier-Stieltjes transform"
Ulf Rehmann (talk | contribs) m (moved Fourier–Stieltjes transform to Fourier-Stieltjes transform: ascii title) |
(→References: Gnedenko: internal link) |
||
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Bochner, "Lectures on Fourier integrals" , Princeton Univ. Press (1959) (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Zygmund, "Trigonometric series" , '''2''' , Cambridge Univ. Press (1988)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> B.V. Gnedenko, "The theory of probability" , Chelsea, reprint (1962) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Bochner, "Lectures on Fourier integrals" , Princeton Univ. Press (1959) (Translated from German)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A. Zygmund, "Trigonometric series" , '''2''' , Cambridge Univ. Press (1988)</TD></TR> |
| + | <TR><TD valign="top">[3]</TD> <TD valign="top"> B.V. Gnedenko, [[Gnedenko, "A course in the theory of probability"|"The theory of probability"]], Chelsea, reprint (1962) (Translated from Russian)</TD></TR></table> | ||
Revision as of 12:20, 1 May 2012
One of the integral transforms (cf. Integral transform) related to the Fourier transform. Let the function  have bounded variation on
have bounded variation on  . The function
. The function
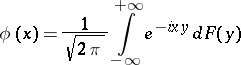 | (*) |
is called the Fourier–Stieltjes transform of  . The function
. The function  determined by the integral (*) is bounded and continuous. Every periodic function
determined by the integral (*) is bounded and continuous. Every periodic function  that can be expanded in an absolutely-convergent Fourier series
that can be expanded in an absolutely-convergent Fourier series  can be written as an integral (*) with
can be written as an integral (*) with  .
.
Formula (*) can be inverted: If  has bounded variation and if
has bounded variation and if
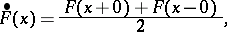 |
then
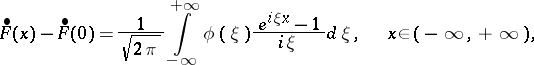 |
where the integral is taken to mean the principal value at 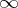 .
.
If one only allows non-decreasing functions of bounded variation as the function  in formula (*), then the set of continuous functions
in formula (*), then the set of continuous functions  thus obtained is completely characterized by the property: For any system of real numbers
thus obtained is completely characterized by the property: For any system of real numbers  ,
,
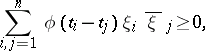 |
whatever the complex numbers 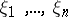 (the Bochner–Khinchin theorem). Such functions are called positive definite. The Fourier–Stieltjes transform is extensively applied in probability theory, where the non-decreasing function
(the Bochner–Khinchin theorem). Such functions are called positive definite. The Fourier–Stieltjes transform is extensively applied in probability theory, where the non-decreasing function
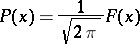 |
is subjected to the additional restrictions  ,
, 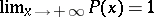 and
and 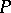 is continuous on the left; it is called a distribution, and
is continuous on the left; it is called a distribution, and
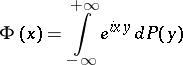 |
is called the characteristic function (of the distribution 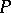 ). The Bochner–Khinchin theorem then expresses a necessary and sufficient condition for a continuous function
). The Bochner–Khinchin theorem then expresses a necessary and sufficient condition for a continuous function  (for which
(for which 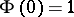 ) to be the characteristic function of a certain distribution.
) to be the characteristic function of a certain distribution.
The Fourier–Stieltjes transform has also been developed in the  -dimensional case.
-dimensional case.
References
| [1] | S. Bochner, "Lectures on Fourier integrals" , Princeton Univ. Press (1959) (Translated from German) |
| [2] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
| [3] | B.V. Gnedenko, "The theory of probability", Chelsea, reprint (1962) (Translated from Russian) |
Fourier-Stieltjes transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier-Stieltjes_transform&oldid=25815