Difference between revisions of "Talk:Sporadic simple group"
From Encyclopedia of Mathematics
(removed table) |
(table test) |
||
| Line 1: | Line 1: | ||
A [[Simple finite group|simple finite group]] that does not belong to any of the known infinite series of simple finite groups. The twenty-six sporadic simple groups are listed in the following table. | A [[Simple finite group|simple finite group]] that does not belong to any of the known infinite series of simple finite groups. The twenty-six sporadic simple groups are listed in the following table. | ||
| + | |||
| + | {| class="wikitable" | ||
| + | ! notation | ||
| + | ! name | ||
| + | ! order | ||
| + | |- | ||
| + | | $M_{11}$ | ||
| + | | | ||
| + | | $2^4.3^2.5.11$ | ||
| + | |- | ||
| + | | $M_{12}$ | ||
| + | | | ||
| + | | $2^6.3^3.5.11$ | ||
| + | |- | ||
| + | | $M_{22}$ | ||
| + | | Mathieu groups | ||
| + | | $2^7.3^2.5.7.11$ | ||
| + | |- | ||
| + | | $M_{23}$ | ||
| + | | | ||
| + | | $2^7.3^2.5.7.11.23$ | ||
| + | |- | ||
| + | | $M_{24}$ | ||
| + | | | ||
| + | | $2^{10}.3^3.5.7.11.23$ | ||
| + | |- | ||
| + | | $J_1$ | ||
| + | | Janko group | ||
| + | | $2^3.3.5.7.11.19$ | ||
| + | |- | ||
| + | | $J_2$, $HJ$ | ||
| + | | Hall–Janko group | ||
| + | | $2^7.3^3.5^2.7$ | ||
| + | |- | ||
| + | | $J_3$, $HJM$ | ||
| + | | Hall–Janko–McKay group | ||
| + | | $2^7.3^5.5.17.19$ | ||
| + | |- | ||
| + | | $J_4$ | ||
| + | | Janko group | ||
| + | | $2^{21}.3^3.5.7.11^3.23.29.31.37.43$ | ||
| + | |- | ||
| + | | $Co_1$ | ||
| + | | | ||
| + | | $2^{21}.3^9.5^4.7^2.11.13.23$ | ||
| + | |- | ||
| + | | $Co_2$ | ||
| + | | Conway groups | ||
| + | | $2^{18}.3^6.5^3.7.11.23$ | ||
| + | |- | ||
| + | | $Co_3$ | ||
| + | | | ||
| + | | $2^{10}.3^7.5^3.7.11.23$ | ||
| + | |- | ||
| + | | $F_{22}$, $M(22)$ | ||
| + | | | ||
| + | | $2^{17}.3^9.5^2.7.11.13$ | ||
| + | |- | ||
| + | | $F_{23}$, $M(23)$ | ||
| + | | Fischer groups | ||
| + | | $2^{18}.3^{13}.5^2.7.11.13.17.23$ | ||
| + | |- | ||
| + | | $F_{24}^\prime$, $M(24)^\prime$ | ||
| + | | | ||
| + | | $2^{21}.3^{16}.5^2.7^3.11.13.17.23.29$ | ||
| + | |- | ||
| + | | $HS$ | ||
| + | | Higman–Sims group | ||
| + | | $2^9.3^2.5^3.7.11$ | ||
| + | |- | ||
| + | | $He$, $HHM$ | ||
| + | | Held–Higman–McKay | ||
| + | | $2^{10}.2^3.5^2.7^3.17$ | ||
| + | |- | ||
| + | | $Suz$ | ||
| + | | Suzuki group | ||
| + | | $2^{13}.3^7.5^2.7.11.13$ | ||
| + | |- | ||
| + | | $M^c$ | ||
| + | | McLaughlin group | ||
| + | | $2^7.3^6.5^3.7.11$ | ||
| + | |- | ||
| + | | $Ly$ | ||
| + | | Lyons group | ||
| + | | $2^8.3^7.5^6.7.11.31.37.67$ | ||
| + | |- | ||
| + | | $Ru$ | ||
| + | | Rudvalis group | ||
| + | | $2^{14}.3^3.5^3.7.13.29$ | ||
| + | |- | ||
| + | | $O'N$, $O'NS$ | ||
| + | | O'Nan–Sims | ||
| + | | $2^9.3^4.5.7^3.11.19.31$ | ||
| + | |- | ||
| + | | $F_1$, $M$ | ||
| + | | Monster, Fischer–Griess group | ||
| + | | $2^{46}.3^{20}.5^9.7^6.11^2.13^3.17.19.23.29.31.41.47.59.71$ | ||
| + | |- | ||
| + | | $F_2$, $B$ | ||
| + | | Baby monster | ||
| + | | $2^{41}.3^{13}.5^6.7^2.11.13.17.19.23.31.47$ | ||
| + | |- | ||
| + | | $F_3$, $E$, $Th$ | ||
| + | | Thompson group | ||
| + | | $2^{15}.3^{10}.5^3.7^2.13.19.31$ | ||
| + | |- | ||
| + | | $F_5$, $D$, $HN$ | ||
| + | | Harada–Norton group | ||
| + | | $2^{14}.3^6.5^6.7.11.19$ | ||
| + | |} | ||
====References==== | ====References==== | ||
Revision as of 16:32, 30 April 2012
A simple finite group that does not belong to any of the known infinite series of simple finite groups. The twenty-six sporadic simple groups are listed in the following table.
| notation | name | order |
|---|---|---|
| $M_{11}$ | $2^4.3^2.5.11$ | |
| $M_{12}$ | $2^6.3^3.5.11$ | |
| $M_{22}$ | Mathieu groups | $2^7.3^2.5.7.11$ |
| $M_{23}$ | $2^7.3^2.5.7.11.23$ | |
| $M_{24}$ | $2^{10}.3^3.5.7.11.23$ | |
| $J_1$ | Janko group | $2^3.3.5.7.11.19$ |
| $J_2$, $HJ$ | Hall–Janko group | $2^7.3^3.5^2.7$ |
| $J_3$, $HJM$ | Hall–Janko–McKay group | $2^7.3^5.5.17.19$ |
| $J_4$ | Janko group | $2^{21}.3^3.5.7.11^3.23.29.31.37.43$ |
| $Co_1$ | $2^{21}.3^9.5^4.7^2.11.13.23$ | |
| $Co_2$ | Conway groups | $2^{18}.3^6.5^3.7.11.23$ |
| $Co_3$ | $2^{10}.3^7.5^3.7.11.23$ | |
| $F_{22}$, $M(22)$ | $2^{17}.3^9.5^2.7.11.13$ | |
| $F_{23}$, $M(23)$ | Fischer groups | $2^{18}.3^{13}.5^2.7.11.13.17.23$ |
| $F_{24}^\prime$, $M(24)^\prime$ | $2^{21}.3^{16}.5^2.7^3.11.13.17.23.29$ | |
| $HS$ | Higman–Sims group | $2^9.3^2.5^3.7.11$ |
| $He$, $HHM$ | Held–Higman–McKay | $2^{10}.2^3.5^2.7^3.17$ |
| $Suz$ | Suzuki group | $2^{13}.3^7.5^2.7.11.13$ |
| $M^c$ | McLaughlin group | $2^7.3^6.5^3.7.11$ |
| $Ly$ | Lyons group | $2^8.3^7.5^6.7.11.31.37.67$ |
| $Ru$ | Rudvalis group | $2^{14}.3^3.5^3.7.13.29$ |
| $O'N$, $O'NS$ | O'Nan–Sims | $2^9.3^4.5.7^3.11.19.31$ |
| $F_1$, $M$ | Monster, Fischer–Griess group | $2^{46}.3^{20}.5^9.7^6.11^2.13^3.17.19.23.29.31.41.47.59.71$ |
| $F_2$, $B$ | Baby monster | $2^{41}.3^{13}.5^6.7^2.11.13.17.19.23.31.47$ |
| $F_3$, $E$, $Th$ | Thompson group | $2^{15}.3^{10}.5^3.7^2.13.19.31$ |
| $F_5$, $D$, $HN$ | Harada–Norton group | $2^{14}.3^6.5^6.7.11.19$ |
References
| [1] | S.A. Syskin, "Abstract properties of the simple sporadic groups" Russian Math. Surveys , 35 : 5 (1980) pp. 209–246 Uspekhi Mat. Nauk , 35 : 5 (1980) pp. 181–212 |
| [2] | M. Aschbacher, "The finite simple groups and their classification" , Yale Univ. Press (1980) |
Comments
The recent classification of the finite simple groups (1981) has led to the conclusion that — up to a uniqueness proof for the Monster as the only simple group of its order with certain additional properties — every non-Abelian finite simple group is isomorphic to: an alternating group on at least  letters, a group of (twisted or untwisted) Lie type, or one of the above
letters, a group of (twisted or untwisted) Lie type, or one of the above 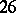 sporadic groups. See [a2] for a discussion of the proof.
sporadic groups. See [a2] for a discussion of the proof.
References
| [a1] | J.H. Conway, R.T. Curtis, S.P. Norton, R.A. Parker, R.A. Wilson, "Atlas of finite groups" , Clarendon Press (1985) |
| [a2] | D. Gorenstein, "Finite simple groups. An introduction to their classification" , Plenum (1982) |
How to Cite This Entry:
Sporadic simple group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sporadic_simple_group&oldid=25777
Sporadic simple group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sporadic_simple_group&oldid=25777