|
|
| Line 1: |
Line 1: |
| − | A [[Simple finite group|simple finite group]] that does not belong to any of the known infinite series of simple finite groups. The twenty-six sporadic simple groups are listed in the following table.''''''<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1">notation</td> <td colname="2" style="background-color:white;" colspan="1">name</td> <td colname="3" style="background-color:white;" colspan="1">order</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868701.png" /></td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868702.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868703.png" /></td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868704.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868705.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Mathieu groups</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868706.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868707.png" /></td> <td colname="2" style="background-color:white;" | + | A [[Simple finite group|simple finite group]] that does not belong to any of the known infinite series of simple finite groups. The twenty-six sporadic simple groups are listed in the following table. |
| − | colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868708.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s0868709.png" /></td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687010.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687011.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Janko group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687012.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687013.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687014.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Hall–Janko group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687015.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687016.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687017.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Higman–Janko–McKay group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687018.png" /></td> </tr> <tr> <td colname="1" style="background-color:white
| |
| − | ;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687019.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Janko group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687020.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687021.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687022.png" /></td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687023.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687024.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687025.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Conway groups</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687026.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687027.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687028.png" /></td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687029.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/
| |
| − | s086870/s08687031.png" /></td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687032.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687033.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687034.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Fischer groups</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687035.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687036.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687037.png" /></td> <td colname="2" style="background-color:white;" colspan="1"></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687038.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687039.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Higman–Sims group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687040.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687041.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687042.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Held–Higman–McKay group</td> <td colname="3" style="background-c
| |
| − | olor:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687043.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687044.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Suzuki group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687045.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687046.png" /></td> <td colname="2" style="background-color:white;" colspan="1">McLaughlin group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687047.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687048.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Lyons group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687049.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687050.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Rudvalis group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687051.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687052.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687053.png" /></td> <td colname="2" style="backgrou
| |
| − | nd-color:white;" colspan="1">O'Nan–Sims group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687054.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687055.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687056.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Monster, Fischer–Griess group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687057.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687058.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687059.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Baby monster</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687060.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687061.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687062.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687063.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Thompson group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687064.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687065.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s08
| |
| − | 6870/s08687066.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687067.png" /></td> <td colname="2" style="background-color:white;" colspan="1">Harada–Norton group</td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s086/s086870/s08687068.png" /></td> </tr> </tbody> </table>
| |
| − | | |
| − | </td></tr> </table>
| |
| | | | |
| | ====References==== | | ====References==== |
Revision as of 15:35, 30 April 2012
A simple finite group that does not belong to any of the known infinite series of simple finite groups. The twenty-six sporadic simple groups are listed in the following table.
References
| [1] | S.A. Syskin, "Abstract properties of the simple sporadic groups" Russian Math. Surveys , 35 : 5 (1980) pp. 209–246 Uspekhi Mat. Nauk , 35 : 5 (1980) pp. 181–212 |
| [2] | M. Aschbacher, "The finite simple groups and their classification" , Yale Univ. Press (1980) |
The recent classification of the finite simple groups (1981) has led to the conclusion that — up to a uniqueness proof for the Monster as the only simple group of its order with certain additional properties — every non-Abelian finite simple group is isomorphic to: an alternating group on at least  letters, a group of (twisted or untwisted) Lie type, or one of the above
letters, a group of (twisted or untwisted) Lie type, or one of the above 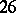 sporadic groups. See [a2] for a discussion of the proof.
sporadic groups. See [a2] for a discussion of the proof.
References
| [a1] | J.H. Conway, R.T. Curtis, S.P. Norton, R.A. Parker, R.A. Wilson, "Atlas of finite groups" , Clarendon Press (1985) |
| [a2] | D. Gorenstein, "Finite simple groups. An introduction to their classification" , Plenum (1982) |
How to Cite This Entry:
Sporadic simple group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Sporadic_simple_group&oldid=25776
 letters, a group of (twisted or untwisted) Lie type, or one of the above
letters, a group of (twisted or untwisted) Lie type, or one of the above 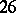 sporadic groups. See [a2] for a discussion of the proof.
sporadic groups. See [a2] for a discussion of the proof.