Difference between revisions of "Non-atomic measure"
From Encyclopedia of Mathematics
(Importing text file) |
(→References: Feller: internal link) |
||
| Line 11: | Line 11: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Feller, | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''2''' , Wiley (1971) pp. 135</TD></TR></table> |
Revision as of 18:32, 26 April 2012
A measure 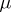 on a measurable space
on a measurable space 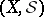 for which there are no atoms of positive measure, i.e. sets
for which there are no atoms of positive measure, i.e. sets 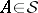 with
with 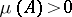 for which
for which 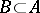 and
and 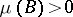 imply
imply  .
.
Comments
An atom in a measure space 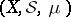 is a set
is a set 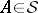 for which i)
for which i)  ; and ii)
; and ii) 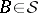 and
and 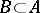 imply either
imply either 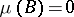 or
or 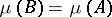 . See also Atom.
. See also Atom.
A measure space 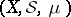 is called non-atomic if no element of
is called non-atomic if no element of 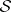 is an atom. In probability theory measure spaces build up completely from atoms, i.e. using atomic measures, frequently occur, cf. Atomic distribution.
is an atom. In probability theory measure spaces build up completely from atoms, i.e. using atomic measures, frequently occur, cf. Atomic distribution.
A probability 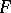 decomposes as a sum
decomposes as a sum 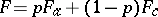 ,
, 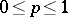 , where
, where 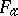 is an atomic distribution and
is an atomic distribution and 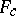 a continuous distribution, i.e. a non-atomic one. This goes by the name Jordan decomposition theorem.
a continuous distribution, i.e. a non-atomic one. This goes by the name Jordan decomposition theorem.
References
| [a1] | W. Feller, "An introduction to probability theory and its applications", 2 , Wiley (1971) pp. 135 |
How to Cite This Entry:
Non-atomic measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-atomic_measure&oldid=25537
Non-atomic measure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-atomic_measure&oldid=25537
This article was adapted from an original article by N.N. Vorob'ev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article