Difference between revisions of "Grothendieck group"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
|||
| Line 1: | Line 1: | ||
''of an additive category'' | ''of an additive category'' | ||
| − | An Abelian group that is assigned to an additive category by a universal additive mapping property. More exactly, let | + | An Abelian group that is assigned to an additive category by a universal additive mapping property. More exactly, let $C$ be a small [[Additive category|additive category]] with set of objects $\mathrm{Ob}(C)$ and let $G$ be an Abelian group. A mapping $\phi: \mathrm{Ob}(C) \to G$ is said to be additive if for any exact sequence $0 \to L \to M \to N \to 0$ in $C$, the relation $\phi(M)=\phi(L)+\phi(N)$ is valid. There exists a group $K(C)$, called the Grothendieck group of $C$, and an additive mapping $k:\mathrm{Ob}(C)\to K(C)$, known as the universal mapping, such that for any additive mapping $\mathrm{Ob}(C) \to G$, there exists a unique homomorphism $\xi: K(C) \to G$ that satisfies the condition $\phi=\xi \circ k$. |
| − | This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See [[K-functor|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g045/g045170/g04517013.png" />-functor]] in algebraic geometry. The group | + | This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See [[K-functor|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g045/g045170/g04517013.png" />-functor]] in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$. |
| − | + | If $X$ is a topological space, then the Grothendieck group of the additive category of vector bundles over $X$ is an invariant of the space, studied in (topological) [[K-theory|K-theory]]. If $C$ is the category of non-degenerate symmetric bilinear forms on linear spaces over a field $k$, then $K(C)$ is the Witt–Grothendieck group of $k$ (cf. [[Witt ring|Witt ring]]). | |
| − | |||
| − | If | ||
====References==== | ====References==== | ||
Revision as of 19:42, 16 April 2012
of an additive category
An Abelian group that is assigned to an additive category by a universal additive mapping property. More exactly, let $C$ be a small additive category with set of objects $\mathrm{Ob}(C)$ and let $G$ be an Abelian group. A mapping $\phi: \mathrm{Ob}(C) \to G$ is said to be additive if for any exact sequence $0 \to L \to M \to N \to 0$ in $C$, the relation $\phi(M)=\phi(L)+\phi(N)$ is valid. There exists a group $K(C)$, called the Grothendieck group of $C$, and an additive mapping $k:\mathrm{Ob}(C)\to K(C)$, known as the universal mapping, such that for any additive mapping $\mathrm{Ob}(C) \to G$, there exists a unique homomorphism $\xi: K(C) \to G$ that satisfies the condition $\phi=\xi \circ k$.
This construction was first studied by A. Grothendieck for the categories of coherent and locally free sheaves on schemes in proving the Riemann–Roch theorem. See 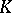 -functor in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$.
-functor in algebraic geometry. The group $K(C)$ is uniquely defined (up to isomorphism) and can be given by generators — to each object $L \in C$, there corresponds a generator $[L]$ — and by the relations $[L]-[N]-[M]=0$ for each exact sequence $0 \to L \to M \to N \to 0$.
If $X$ is a topological space, then the Grothendieck group of the additive category of vector bundles over $X$ is an invariant of the space, studied in (topological) K-theory. If $C$ is the category of non-degenerate symmetric bilinear forms on linear spaces over a field $k$, then $K(C)$ is the Witt–Grothendieck group of $k$ (cf. Witt ring).
References
| [1] | R. Swan, "The Grothendieck ring of a finite group" Topology , 2 (1963) pp. 85–110 MR0153722 Zbl 0119.02905 |
| [2] | A. Borel, J.P. Serre, "Le théorème de Riemann–Roch" Bull. Soc. Math. France , 86 (1958) pp. 97–136 MR116022 Zbl 0091.33004 |
| [3] | M.F. Atiyah, "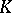 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [4] | H. Bass, "Lectures on topics in algebraic  -theory" , Tata Inst. (1966) -theory" , Tata Inst. (1966) |
| [5] | S. Lang, "Algebra" , Addison-Wesley (1974) MR0783636 Zbl 0712.00001 |
Comments
One also associates a Grothendieck group 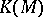 to any commutative monoid as the solution of the universal problem posed by additive mappings of
to any commutative monoid as the solution of the universal problem posed by additive mappings of 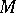 into Abelian groups. It is the Abelian group with generators
into Abelian groups. It is the Abelian group with generators 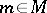 and relations
and relations 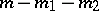 , for all
, for all 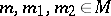 such that
such that 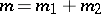 in
in 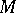 . Taking, for instance, the monoid of isomorphism classes of vector bundles over a topological space
. Taking, for instance, the monoid of isomorphism classes of vector bundles over a topological space  (with the monoid addition induced by the direct sum) one again obtains the topological
(with the monoid addition induced by the direct sum) one again obtains the topological 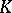 -group
-group 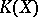 .
.
When considering an additive category 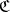 in which not every short exact sequence splits, there are two possible natural associated Grothendieck groups. Both are Abelian groups generated by the isomorphism classes of objects of
in which not every short exact sequence splits, there are two possible natural associated Grothendieck groups. Both are Abelian groups generated by the isomorphism classes of objects of 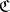 . For the first there is a relation
. For the first there is a relation 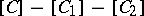 whenever
whenever 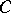 is isomorphic to
is isomorphic to  , and for the second there is a relation
, and for the second there is a relation 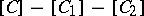 whenever there is a short exact sequence
whenever there is a short exact sequence 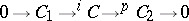 . (Such a short exact sequence splits if there is a morphism
. (Such a short exact sequence splits if there is a morphism 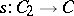 such that
such that  .) Both notions occur in the literature.
.) Both notions occur in the literature.
The Grothendieck group 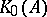 defined by the additive category of finitely-generated projective modules over
defined by the additive category of finitely-generated projective modules over 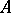 (in which every short exact sequence splits of course) is sometimes called the Grothendieck group of the ring
(in which every short exact sequence splits of course) is sometimes called the Grothendieck group of the ring 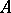 . Cf. also Algebraic
. Cf. also Algebraic 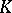 -theory. Another important example of a Grothendieck group is the Picard group
-theory. Another important example of a Grothendieck group is the Picard group 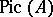 of a ring (or of a scheme). It is the Grothendieck group associated to the commutative monoid of isomorphism classes of rank 1 projective modules over
of a ring (or of a scheme). It is the Grothendieck group associated to the commutative monoid of isomorphism classes of rank 1 projective modules over  with the addition induced by the tensor prodect over
with the addition induced by the tensor prodect over 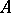 .
.
References
| [a1] | H. Bass, "Algebraic  -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
| [a2] | M. Karoubi, "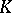 -theory" , Springer (1978) MR0488029 Zbl 0382.55002 -theory" , Springer (1978) MR0488029 Zbl 0382.55002 |
| [a3] | J. Berrick, "An approach to algebraic 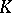 -theory" , Pitman (1982) MR649409 -theory" , Pitman (1982) MR649409 |
Grothendieck group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grothendieck_group&oldid=24624