Difference between revisions of "Weil algebra of a Lie algebra"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 24: | Line 24: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Cartan, "Cohomologie réelle d'un espace fibré principal differentiable" , ''Sem. H. Cartan 1949/50, Exp. 19–20'' (1950)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.L. Dupont, F.W. Kamber, "On a generalization of Cheeger–Chern–Simons classes" ''Illinois J. Math.'' , '''34''' (1990) {{MR|1046564}} {{ZBL|0724.57018}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> F.W. Kamber, Ph. Tondeur, "Foliated bundles and characteristic classes" , ''Lecture Notes in Mathematics'' , '''493''' , Springer (1975) {{MR|0402773}} {{MR|0385886}} {{ZBL|0311.57011}} {{ZBL|0308.57011}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> F.W. Kamber, Ph. Tondeur, "Semi-simplicial Weil algebras and characteristic classes" ''Tôhoku Math. J.'' , '''30''' (1978) pp. 373–422 {{MR|0509023}} {{ZBL|0398.57006}} </TD></TR></table> |
Revision as of 17:02, 15 April 2012
Let  be a connected Lie group with Lie algebra
be a connected Lie group with Lie algebra  . The Weil algebra
. The Weil algebra  of
of  was first introduced in a series of seminars by H. Cartan [a1], in part based on some unpublished work of A. Weil. As a differential graded algebra, it is given by the tensor product
was first introduced in a series of seminars by H. Cartan [a1], in part based on some unpublished work of A. Weil. As a differential graded algebra, it is given by the tensor product
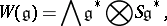 |
where  and
and  denote the exterior and symmetric algebras, respectively (cf. also Exterior algebra; Symmetric algebra).
denote the exterior and symmetric algebras, respectively (cf. also Exterior algebra; Symmetric algebra).
The Weil algebra and its generalizations have been studied extensively by F.W. Kamber and Ph. Tondeur [a3] [a4]. Let  be a maximal compact subgroup, with
be a maximal compact subgroup, with  denoting the Lie algebra of
denoting the Lie algebra of 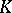 . The relative Weil algebra for
. The relative Weil algebra for  is defined by
is defined by
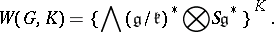 |
With regards to the universal classifying bundle 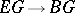 (cf. also Bundle; Classifying space; Universal space), there are canonical isomorphisms in cohomology
(cf. also Bundle; Classifying space; Universal space), there are canonical isomorphisms in cohomology
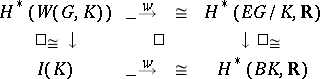 |
where 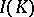 denotes the
denotes the 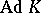 -invariant polynomials. For a given integer
-invariant polynomials. For a given integer  , one has the ideal
, one has the ideal
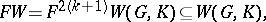 |
generated by 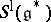 , for
, for 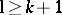 . This leads to the truncated Weil algebra
. This leads to the truncated Weil algebra
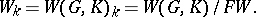 |
The cohomology  plays a prominent role in the study of secondary characteristic classes (cf. also Characteristic class) of foliations and foliated bundles [a3] (see also [a2]).
plays a prominent role in the study of secondary characteristic classes (cf. also Characteristic class) of foliations and foliated bundles [a3] (see also [a2]).
References
| [a1] | H. Cartan, "Cohomologie réelle d'un espace fibré principal differentiable" , Sem. H. Cartan 1949/50, Exp. 19–20 (1950) |
| [a2] | J.L. Dupont, F.W. Kamber, "On a generalization of Cheeger–Chern–Simons classes" Illinois J. Math. , 34 (1990) MR1046564 Zbl 0724.57018 |
| [a3] | F.W. Kamber, Ph. Tondeur, "Foliated bundles and characteristic classes" , Lecture Notes in Mathematics , 493 , Springer (1975) MR0402773 MR0385886 Zbl 0311.57011 Zbl 0308.57011 |
| [a4] | F.W. Kamber, Ph. Tondeur, "Semi-simplicial Weil algebras and characteristic classes" Tôhoku Math. J. , 30 (1978) pp. 373–422 MR0509023 Zbl 0398.57006 |
Weil algebra of a Lie algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weil_algebra_of_a_Lie_algebra&oldid=24593