Difference between revisions of "Stefan problem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | A problem that arises when studying physical processes related to phase transformation of matter. The simplest two-phase Stefan problem is formulated in thermo-physical terms as follows ([[#References|[1]]], [[#References|[2]]]): Find the distribution of the temperature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087600/s0876001.png" /> and the law of motion of the dividing boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087600/s0876002.png" /> (for example, the boundary | + | A problem that arises when studying physical processes related to phase transformation of matter. The simplest two-phase Stefan problem is formulated in thermo-physical terms as follows ([[#References|[1]]], [[#References|[2]]]): Find the distribution of the temperature <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087600/s0876001.png" /> and the law of motion of the dividing boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087600/s0876002.png" /> (for example, the boundary "ice-water" in freezing water) from the equation of heat conductivity: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087600/s0876003.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087600/s0876003.png" /></td> </tr></table> | ||
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J. Stefan, "Ueber einige Probleme der Theorie der Wärmeleitung" ''Sitzungsber. Wiener Akad. Math. Naturwiss. Abt. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s087/s087600/s08760021.png" />'' , '''98''' (1889) pp. 473–484 {{MR|}} {{ZBL|21.1197.01}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian) {{MR|0165209}} {{ZBL|0111.29008}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> O.A. Oleinik, "A method of solution of the general Stefan problem" ''Soviet Math. Dokl.'' , '''1''' : 6 (1960) pp. 1350–1354 ''Dokl. Akad. Nauk SSSR'' , '''135''' : 5 (1960) pp. 1054–1057 {{MR|0125341}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> B.M. Budak, A.B. Uspenskii, "A difference method with front straightening for solving Stefan-type problems" ''USSR Comp. Math. Math. Phys.'' , '''9''' : 6 (1969) pp. 83–103 ''Zh. Vychisl. Mat. i Mat. Fiz.'' , '''9''' : 6 (1969) pp. 1299–1315 {{MR|}} {{ZBL|0239.65072}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> B.M. Budak, M.Z. Moskal, "On a classical solution of a multidimensional multiphase Stefan type problem in a domain with piecewise smooth boundary" ''Soviet Math. Dokl.'' , '''13''' : 2 (1970) pp. 427–432 ''Dokl. Akad. Nauk SSSR'' , '''191''' : 4 (1970) pp. 751–754 {{MR|}} {{ZBL|0215.45701}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> B.M. Budak, F.P. Vasil'ev, A.B. Uspenskii, "Difference methods for solving certain boundary value problems of Stefan type" , ''Numerical Methods in Gas Dynamics'' , Moscow (1965) pp. 139–183 (In Russian) {{MR|0207310}} {{ZBL|}} </TD></TR></table> |
| Line 48: | Line 48: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Stefan, "Ueber die Theorie der Eisbildung, insbesondere ueber die Eisbildung im Polarmeere" ''Ann. Physik Chemie'' , '''42''' (1891) pp. 269–286 {{MR|}} {{ZBL|23.1188.04}} {{ZBL|21.1198.01}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G. Lamé, B.P. Clapeyron, "Mémoire sur la solidification par refroidissement d'un globe liquide" ''Ann. Chimie Physique'' , '''47''' (1831) pp. 250–256</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> L.I. Rubinstein, "The Stefan problem" , Amer. Math. Soc. (1971) (Translated from Russian) {{MR|0351348}} {{ZBL|0952.35162}} {{ZBL|0866.35146}} {{ZBL|0488.35012}} {{ZBL|0491.35084}} {{ZBL|0456.35096}} {{ZBL|0434.35086}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) {{MR|0181836}} {{ZBL|0144.34903}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.R. Cannon, "The one-dimensional heat equation" , Addison-Wesley (1984) {{MR|0747979}} {{ZBL|0567.35001}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> S.L. Kamenomostskaya, "On the Stefan problem" ''Mat. Sb.'' , '''53''' (1961) pp. 489–514 (In Russian)</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> A. Friedman, "The Stefan problem in several space variables" ''Trans. Amer. Math. Soc.'' , '''132''' (1968) pp. 51–87 {{MR|0227625}} {{ZBL|0182.43201}} {{ZBL|0162.41903}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> A. Friedman, "One dimensional Stefan problems with nonmonotone free boundary" ''Trans. Amer. Math. Soc.'' , '''133''' (1968) pp. 89–114 {{MR|0227626}} {{ZBL|0162.42001}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> M. Frémond, "Variational formulation of the Stefan problem. Coupled Stefan problem - frost propagation in porous media" , ''Computational Methods in Nonlinear Mechanics'' , Univ. Texas at Austin (1974) pp. 341–349 {{MR|0398299}} {{ZBL|0316.76063}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> G. Duvaut, "Résolution d'un problème de Stefan (Fusion d'un bloc de glace a zero degrées)" ''C.R. Acad. Sci. Paris'' , '''276''' (1973) pp. 1461–1463</TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> A. Fasano, M. Primicerio, "New results on some classical parabolic free-bounded problems" ''Quart. Appl. Math.'' , '''38''' (1981) pp. 439–460</TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> A. Fasano, M. Primicerio, "A critical case for the solvability of Stefan-like problems" ''Math. Methods Appl. Sci.'' , '''5''' (1983) pp. 84–96 {{MR|0690897}} {{ZBL|0526.35078}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> A. Fasano, S.D. Howison, M. Primicerio, J.R. Ockendon, "On the singularities of the one-dimensional Stefan problems with supercooling" ''Quart. Appl. Math.'' (to appear)</TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> A.M. Meirmanov, "An example of nonexistence of a classical solution of the Stefan problem" ''Soviet Math. Dokl.'' , '''23''' (1981) pp. 564–566 ''Dokl. Akad. Nauk USSR'' , '''258''' : 3 (1981) pp. 547–550 {{MR|620870}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> M. Primicerio, "Mushy regions in phase-change problems" K.H. Hoffmann (ed.) R. Gorenflo (ed.) , ''Applied Nonlinear Functional analysis: Variational Methods and Ill-Posed Problems'' , Verlag Peter Lang (1983) pp. 251–269 {{MR|0685609}} {{ZBL|0518.35087}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> A. Fasano, M. Primicerio, "A parabolic-hyperbolic free boundary problem" ''SIAM J. Math. Anal.'' , '''17''' (1986) pp. 67–73 {{MR|0819213}} {{ZBL|0594.35092}} </TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> M. Niezgodka, "Stefan-like problems" A. Fasano (ed.) M. Primicerio (ed.) , ''Free boundary problems: theory and application'' , '''1–2''' , Pitman (1983) pp. 321–348 {{MR|0714922}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> G.H. Meyer, "Numerical methods for free boundary problems" A. Fasano (ed.) M. Primicerio (ed.) , ''Free boundary problems: theory and application'' , '''1–2''' , Pitman (1983) pp. 590–600 {{MR|}} {{ZBL|0513.65076}} </TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> R.H. Nochetto, "Numerical solutions for free boundary problems" K.H. Hoffmann (ed.) J. Sprekels (ed.) , ''Free boundary problems: theory and applications'' , '''5–6''' , Longman (To appear)</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> D.G. Aronson, "The porous medium equation" A. Fasano (ed.) M. Primicerio (ed.) , ''Nonlinear diffusion problems'' , ''Lect. notes in math.'' , '''1224''' , Springer (1986) pp. 1–46 {{MR|0877986}} {{ZBL|0626.76097}} </TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> D.A. Tarzia, "A bibliography on moving-free boundary problems for the heat-diffusion equation" , ''Prog. Naz. "Equazioni di evoluzione e applicazioni fisico-matematiche" '' , Firenze (1988) {{MR|1007840}} {{ZBL|0694.35221}} </TD></TR></table> |
Revision as of 17:01, 15 April 2012
A problem that arises when studying physical processes related to phase transformation of matter. The simplest two-phase Stefan problem is formulated in thermo-physical terms as follows ([1], [2]): Find the distribution of the temperature 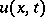 and the law of motion of the dividing boundary
and the law of motion of the dividing boundary 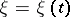 (for example, the boundary "ice-water" in freezing water) from the equation of heat conductivity:
(for example, the boundary "ice-water" in freezing water) from the equation of heat conductivity:
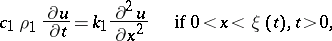 |
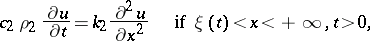 |
with the boundary condition
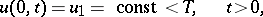 |
the initial condition
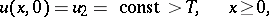 |
and the conditions on the freezing boundary
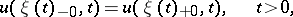 |
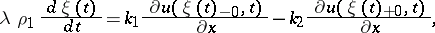 |
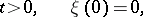 |
where 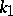 and
and 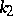 are the coefficients of heat conductivity,
are the coefficients of heat conductivity, 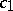 and
and 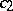 are the specific heats,
are the specific heats, 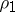 and
and 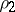 are the densities of the solid and the corresponding liquid phase,
are the densities of the solid and the corresponding liquid phase, 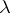 is the latent heat of melting per unit of mass, and
is the latent heat of melting per unit of mass, and 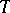 is the temperature of freezing. This problem has a self-similar solution
is the temperature of freezing. This problem has a self-similar solution 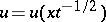 ,
, 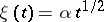 ,
, 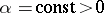 .
.
A sufficiently-general formulation of the Stefan problem in the three-dimensional spatial case reduces to a boundary value problem for a quasi-linear parabolic equation of the second order with piecewise-continuous coefficients having discontinuities of the first kind on previously-unknown but sought-for surfaces, on which the value of the required function is defined, and which also satisfy the differential Stefan condition. The existence and uniqueness of classical and generalized solutions of the Stefan problem have been studied ([3]–[6]); for methods of approximate solution of the Stefan problem, see [2], [4], [6].
One of the first to study this type of problem was J. Stefan [1].
References
| [1] | J. Stefan, "Ueber einige Probleme der Theorie der Wärmeleitung" Sitzungsber. Wiener Akad. Math. Naturwiss. Abt. 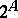 , 98 (1889) pp. 473–484 Zbl 21.1197.01 , 98 (1889) pp. 473–484 Zbl 21.1197.01 |
| [2] | A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian) MR0165209 Zbl 0111.29008 |
| [3] | O.A. Oleinik, "A method of solution of the general Stefan problem" Soviet Math. Dokl. , 1 : 6 (1960) pp. 1350–1354 Dokl. Akad. Nauk SSSR , 135 : 5 (1960) pp. 1054–1057 MR0125341 |
| [4] | B.M. Budak, A.B. Uspenskii, "A difference method with front straightening for solving Stefan-type problems" USSR Comp. Math. Math. Phys. , 9 : 6 (1969) pp. 83–103 Zh. Vychisl. Mat. i Mat. Fiz. , 9 : 6 (1969) pp. 1299–1315 Zbl 0239.65072 |
| [5] | B.M. Budak, M.Z. Moskal, "On a classical solution of a multidimensional multiphase Stefan type problem in a domain with piecewise smooth boundary" Soviet Math. Dokl. , 13 : 2 (1970) pp. 427–432 Dokl. Akad. Nauk SSSR , 191 : 4 (1970) pp. 751–754 Zbl 0215.45701 |
| [6] | B.M. Budak, F.P. Vasil'ev, A.B. Uspenskii, "Difference methods for solving certain boundary value problems of Stefan type" , Numerical Methods in Gas Dynamics , Moscow (1965) pp. 139–183 (In Russian) MR0207310 |
Comments
The problem was formulated by Stefan in [1] and [a1], but it was first studied many years before by G. Lamé and B.D. Clapeyron in a joint paper [a2].
The mathematical theory of the classical Stefan problem in one space dimension has been developed between 1947 and 1967 mainly by L. Rubinstein (see [a3]), A. Friedman (see [a4]), Jiang Li-shang, J.R. Cannon and C.D. Hill (see [a5]).
Other fundamental papers on the generalized solution of the Stefan problem are [a6]–[a8]. The reduction to a variational inequality has also received great attention [a9], [a10].
In the 1970's and 1980's many generalizations have been studied, not only concerning the conditions on the free boundary or the differential equation (see Stefan condition), but also considering the possibility of supercooling or superheating phenomena, possibly producing singularities of the solution (see e.g. [a11]–[a13]) or the occurrence of regions (called mushy regions) where the temperature is equal to the melting temperature and in which the thermal energy (or, more precisely, the enthalpy) satisfies a hyperbolic equation (see [a14]–[a16]).
Important references are also the survey papers [a17] (general theory), [a18]–[a19] (numerical methods).
The Stefan problem is related to many other free boundary problems, like the problem of gas flow through porous media (see [a20]). A useful guide to the extensive literature on the Stefan problem is [a21].
See also Differential equation, partial, free boundaries; Differential equation, partial, discontinuous coefficients; Differential equation, partial, with singular coefficients.
References
| [a1] | J. Stefan, "Ueber die Theorie der Eisbildung, insbesondere ueber die Eisbildung im Polarmeere" Ann. Physik Chemie , 42 (1891) pp. 269–286 Zbl 23.1188.04 Zbl 21.1198.01 |
| [a2] | G. Lamé, B.P. Clapeyron, "Mémoire sur la solidification par refroidissement d'un globe liquide" Ann. Chimie Physique , 47 (1831) pp. 250–256 |
| [a3] | L.I. Rubinstein, "The Stefan problem" , Amer. Math. Soc. (1971) (Translated from Russian) MR0351348 Zbl 0952.35162 Zbl 0866.35146 Zbl 0488.35012 Zbl 0491.35084 Zbl 0456.35096 Zbl 0434.35086 |
| [a4] | A. Friedman, "Partial differential equations of parabolic type" , Prentice-Hall (1964) MR0181836 Zbl 0144.34903 |
| [a5] | J.R. Cannon, "The one-dimensional heat equation" , Addison-Wesley (1984) MR0747979 Zbl 0567.35001 |
| [a6] | S.L. Kamenomostskaya, "On the Stefan problem" Mat. Sb. , 53 (1961) pp. 489–514 (In Russian) |
| [a7] | A. Friedman, "The Stefan problem in several space variables" Trans. Amer. Math. Soc. , 132 (1968) pp. 51–87 MR0227625 Zbl 0182.43201 Zbl 0162.41903 |
| [a8] | A. Friedman, "One dimensional Stefan problems with nonmonotone free boundary" Trans. Amer. Math. Soc. , 133 (1968) pp. 89–114 MR0227626 Zbl 0162.42001 |
| [a9] | M. Frémond, "Variational formulation of the Stefan problem. Coupled Stefan problem - frost propagation in porous media" , Computational Methods in Nonlinear Mechanics , Univ. Texas at Austin (1974) pp. 341–349 MR0398299 Zbl 0316.76063 |
| [a10] | G. Duvaut, "Résolution d'un problème de Stefan (Fusion d'un bloc de glace a zero degrées)" C.R. Acad. Sci. Paris , 276 (1973) pp. 1461–1463 |
| [a11] | A. Fasano, M. Primicerio, "New results on some classical parabolic free-bounded problems" Quart. Appl. Math. , 38 (1981) pp. 439–460 |
| [a12] | A. Fasano, M. Primicerio, "A critical case for the solvability of Stefan-like problems" Math. Methods Appl. Sci. , 5 (1983) pp. 84–96 MR0690897 Zbl 0526.35078 |
| [a13] | A. Fasano, S.D. Howison, M. Primicerio, J.R. Ockendon, "On the singularities of the one-dimensional Stefan problems with supercooling" Quart. Appl. Math. (to appear) |
| [a14] | A.M. Meirmanov, "An example of nonexistence of a classical solution of the Stefan problem" Soviet Math. Dokl. , 23 (1981) pp. 564–566 Dokl. Akad. Nauk USSR , 258 : 3 (1981) pp. 547–550 MR620870 |
| [a15] | M. Primicerio, "Mushy regions in phase-change problems" K.H. Hoffmann (ed.) R. Gorenflo (ed.) , Applied Nonlinear Functional analysis: Variational Methods and Ill-Posed Problems , Verlag Peter Lang (1983) pp. 251–269 MR0685609 Zbl 0518.35087 |
| [a16] | A. Fasano, M. Primicerio, "A parabolic-hyperbolic free boundary problem" SIAM J. Math. Anal. , 17 (1986) pp. 67–73 MR0819213 Zbl 0594.35092 |
| [a17] | M. Niezgodka, "Stefan-like problems" A. Fasano (ed.) M. Primicerio (ed.) , Free boundary problems: theory and application , 1–2 , Pitman (1983) pp. 321–348 MR0714922 |
| [a18] | G.H. Meyer, "Numerical methods for free boundary problems" A. Fasano (ed.) M. Primicerio (ed.) , Free boundary problems: theory and application , 1–2 , Pitman (1983) pp. 590–600 Zbl 0513.65076 |
| [a19] | R.H. Nochetto, "Numerical solutions for free boundary problems" K.H. Hoffmann (ed.) J. Sprekels (ed.) , Free boundary problems: theory and applications , 5–6 , Longman (To appear) |
| [a20] | D.G. Aronson, "The porous medium equation" A. Fasano (ed.) M. Primicerio (ed.) , Nonlinear diffusion problems , Lect. notes in math. , 1224 , Springer (1986) pp. 1–46 MR0877986 Zbl 0626.76097 |
| [a21] | D.A. Tarzia, "A bibliography on moving-free boundary problems for the heat-diffusion equation" , Prog. Naz. "Equazioni di evoluzione e applicazioni fisico-matematiche" , Firenze (1988) MR1007840 Zbl 0694.35221 |
Stefan problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stefan_problem&oldid=24571