Difference between revisions of "Recursions of higher degrees"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | Recursive definitions (cf. [[Recursive definition|Recursive definition]]) that, in addition to numerical functions, use some functions of higher types as auxiliary objects. For example, in the case of recursion of the second degree such are the | + | Recursive definitions (cf. [[Recursive definition|Recursive definition]]) that, in addition to numerical functions, use some functions of higher types as auxiliary objects. For example, in the case of recursion of the second degree such are the "substituting" functionals of type |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080220/r0802201.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r080/r080220/r0802201.png" /></td> </tr></table> | ||
| − | as well as functionals that can be obtained from these by this recursion. The interesting property of recursion of higher degree is that [[Multiple recursion|multiple recursion]] can be reduced to single recursion using a transition to a higher degree. This forms the basis for the method of reducing multiple recursions to a normal form. It should be borne in mind that the terminology in this field is not definitely established. In particular, the term | + | as well as functionals that can be obtained from these by this recursion. The interesting property of recursion of higher degree is that [[Multiple recursion|multiple recursion]] can be reduced to single recursion using a transition to a higher degree. This forms the basis for the method of reducing multiple recursions to a normal form. It should be borne in mind that the terminology in this field is not definitely established. In particular, the term "recursions of higher degrees" is sometimes taken to mean normal forms of multiple recursions. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> R. Peter, "Recursive functions" , Acad. Press (1967) (Translated from German) {{MR|0219414}} {{ZBL|0154.00601}} </TD></TR></table> |
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. 234 {{MR|1234051}} {{MR|1570642}} {{MR|0051790}} {{ZBL|0875.03002}} {{ZBL|0604.03002}} {{ZBL|0109.00509}} {{ZBL|0047.00703}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> P. Odifreddi, "Classical recursion theory" , North-Holland (1989) pp. Chapt. II; esp. pp. 199ff {{MR|0982269}} {{ZBL|0661.03029}} </TD></TR></table> |
Revision as of 17:01, 15 April 2012
Recursive definitions (cf. Recursive definition) that, in addition to numerical functions, use some functions of higher types as auxiliary objects. For example, in the case of recursion of the second degree such are the "substituting" functionals of type
 |
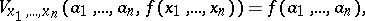as well as functionals that can be obtained from these by this recursion. The interesting property of recursion of higher degree is that multiple recursion can be reduced to single recursion using a transition to a higher degree. This forms the basis for the method of reducing multiple recursions to a normal form. It should be borne in mind that the terminology in this field is not definitely established. In particular, the term "recursions of higher degrees" is sometimes taken to mean normal forms of multiple recursions.
References
| [1] | R. Peter, "Recursive functions" , Acad. Press (1967) (Translated from German) MR0219414 Zbl 0154.00601 |
Comments
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. 234 MR1234051 MR1570642 MR0051790 Zbl 0875.03002 Zbl 0604.03002 Zbl 0109.00509 Zbl 0047.00703 |
| [a2] | P. Odifreddi, "Classical recursion theory" , North-Holland (1989) pp. Chapt. II; esp. pp. 199ff MR0982269 Zbl 0661.03029 |
How to Cite This Entry:
Recursions of higher degrees. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursions_of_higher_degrees&oldid=24547
Recursions of higher degrees. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Recursions_of_higher_degrees&oldid=24547
This article was adapted from an original article by N.V. Belyakin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article