Difference between revisions of "Prenex formula"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 22: | Line 22: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964) {{MR|0164867}} {{ZBL|1173.03001}} {{ZBL|0915.03002}} {{ZBL|0681.03001}} {{ZBL|0534.03001}} {{ZBL|0498.03001}} {{ZBL|0192.01901}} </TD></TR></table> |
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. Chapt. VII, §35 {{MR|1234051}} {{MR|1570642}} {{MR|0051790}} {{ZBL|0875.03002}} {{ZBL|0604.03002}} {{ZBL|0109.00509}} {{ZBL|0047.00703}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Fraissé, "Course of mathematical logic" , '''1''' , Reidel (1973) pp. Sect. 5.1.1ff {{MR|0345784}} {{ZBL|0262.02001}} </TD></TR></table> |
Revision as of 17:00, 15 April 2012
A formula from the restricted predicate calculus having the form
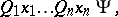 |
where 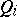 denotes the universal quantifier
denotes the universal quantifier 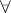 or the existential quantifier
or the existential quantifier 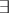 , the variables
, the variables 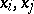 are distinct for
are distinct for 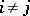 , and
, and 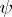 is a formula without quantifiers. Prenex formulas are also called prenex normal forms or prenex forms.
is a formula without quantifiers. Prenex formulas are also called prenex normal forms or prenex forms.
For each formula 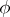 of the language of the restricted predicate calculus there is a prenex formula that is logically equivalent to
of the language of the restricted predicate calculus there is a prenex formula that is logically equivalent to 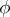 in the classical predicate calculus. The procedure of finding a prenex formula is based on the following equivalences, which can be deduced in the classical predicate calculus:
in the classical predicate calculus. The procedure of finding a prenex formula is based on the following equivalences, which can be deduced in the classical predicate calculus:
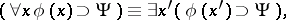 |
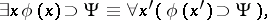 |
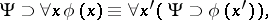 |
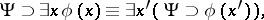 |
 |
 |
where 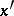 is any variable not appearing as a free variable in
is any variable not appearing as a free variable in 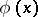 or
or  , and
, and 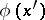 can be obtained from
can be obtained from 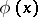 by changing all free appearances of
by changing all free appearances of  to
to 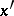 ; the variable
; the variable 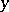 does not appear as a free variable in
does not appear as a free variable in 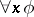 or
or 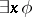 . To use the above equivalences one has to first express all logical operators by
. To use the above equivalences one has to first express all logical operators by  and
and  and then move all quantifiers to the left by applying the equivalences. The prenex formula thus obtained is called the prenex form of the given formula.
and then move all quantifiers to the left by applying the equivalences. The prenex formula thus obtained is called the prenex form of the given formula.
References
| [1] | E. Mendelson, "Introduction to mathematical logic" , v. Nostrand (1964) MR0164867 Zbl 1173.03001 Zbl 0915.03002 Zbl 0681.03001 Zbl 0534.03001 Zbl 0498.03001 Zbl 0192.01901 |
Comments
References
| [a1] | S.C. Kleene, "Introduction to metamathematics" , North-Holland (1950) pp. Chapt. VII, §35 MR1234051 MR1570642 MR0051790 Zbl 0875.03002 Zbl 0604.03002 Zbl 0109.00509 Zbl 0047.00703 |
| [a2] | R. Fraissé, "Course of mathematical logic" , 1 , Reidel (1973) pp. Sect. 5.1.1ff MR0345784 Zbl 0262.02001 |
Prenex formula. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Prenex_formula&oldid=24538