Difference between revisions of "Fold"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.V. Hörmander, "The analysis of linear partial differential operators" , '''3''' , Springer (1985) {{MR|1540773}} {{MR|0781537}} {{MR|0781536}} {{ZBL|0612.35001}} {{ZBL|0601.35001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , '''1''' , Birkhäuser (1985) (Translated from Russian) {{MR|777682}} {{ZBL|0554.58001}} </TD></TR></table> |
Revision as of 16:57, 15 April 2012
A type of singularity of differentiable mappings (cf. Singularities of differentiable mappings).
Let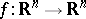 
be a 
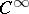-function. Then 
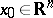is said to be a fold of 
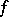if
 |
and if the Hessian of 
at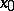 
is not equal to zero (cf. Hessian of a function). This definition can be generalized to the case of a 
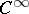-mapping 
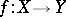between 
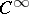-manifolds 
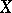and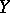 
(necessarily of the same dimension), cf. [a1].
The name derives from the following fact: If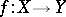 
(with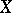 
, 
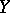and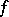 
as above) has a fold at 
, then there are local coordinates 
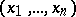in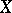 
vanishing at 
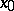and local coordinates 
in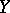 
vanishing at 
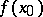such that 
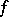has the local representation
 |
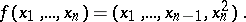References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 3 , Springer (1985) MR1540773 MR0781537 MR0781536 Zbl 0612.35001 Zbl 0601.35001 |
| [a2] | V.I. Arnol'd, S.M. [S.M. Khusein-Zade] Gusein-Zade, A.N. Varchenko, "Singularities of differentiable maps" , 1 , Birkhäuser (1985) (Translated from Russian) MR777682 Zbl 0554.58001 |
How to Cite This Entry:
Fold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fold&oldid=24441
Fold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fold&oldid=24441