Difference between revisions of "Classifying space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 11: | Line 11: | ||
There is a natural mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244088.png" /> corresponding to the addition of a one-dimensional trivial bundle to a vector bundle. The mapping can be regarded as an imbedding, so that it makes sense to consider the union <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244089.png" /> in the inductive limit topology. The spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244090.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244091.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244092.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244093.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244094.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244095.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244096.png" />, etc., are constructed in a completely analogous fashion. These are classifying spaces for stable equivalence classes of bundles given over connected finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244097.png" />-complexes. All these spaces have <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244098.png" />-space structures coming from the operation of Whitney sums of fibre bundles. | There is a natural mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244088.png" /> corresponding to the addition of a one-dimensional trivial bundle to a vector bundle. The mapping can be regarded as an imbedding, so that it makes sense to consider the union <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244089.png" /> in the inductive limit topology. The spaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244090.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244091.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244092.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244093.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244094.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244095.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244096.png" />, etc., are constructed in a completely analogous fashion. These are classifying spaces for stable equivalence classes of bundles given over connected finite <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244097.png" />-complexes. All these spaces have <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244098.png" />-space structures coming from the operation of Whitney sums of fibre bundles. | ||
| − | The term | + | The term "classifying space" is not used solely in connection with fibre bundles. Sometimes classifying space refers to the representing space (object) for an arbitrary representable functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c02244099.png" /> of the homotopy category into the category of sets. An example of such a classifying space is the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c022440100.png" /> which classifies in some sense foliations (cf. [[Foliation|Foliation]]) of codimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c022440101.png" /> on a manifold, or, more generally, Haefliger <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022440/c022440102.png" />-structures on an arbitrary topological space. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.M. Boardman, R.M. Vogt, "Homotopy invariant algebraic structures on topological spaces" , Springer (1973) {{MR|0420609}} {{MR|0420610}} {{ZBL|0285.55012}} </TD></TR></table> |
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) {{MR|0440554}} {{ZBL|0298.57008}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J. Madsen, R.J. Milgram, "The classifying spaces for surgery and cobordism of manifolds" , Princeton Univ. Press (1979) {{MR|0548575}} {{ZBL|0446.57002}} </TD></TR></table> |
Revision as of 16:56, 15 April 2012
The base 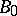 of a universal fibre bundle
of a universal fibre bundle 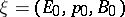 .
.
The universality of the bundle 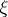 is to be understood in the following sense. Let
is to be understood in the following sense. Let  be the set of equivalence classes (with respect to a notion of isomorphism (covering the identity mapping of
be the set of equivalence classes (with respect to a notion of isomorphism (covering the identity mapping of 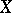 )) of locally trivial bundles over the
)) of locally trivial bundles over the 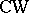 -complex
-complex 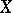 with structure group
with structure group 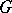 . If
. If 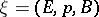 is a locally trivial bundle with structure group
is a locally trivial bundle with structure group 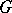 ,
, 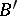 is a topological space and
is a topological space and 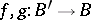 are homotopic mappings, then the induced bundles
are homotopic mappings, then the induced bundles 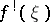 and
and 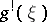 over
over 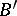 belong to the same class in
belong to the same class in 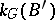 . A locally trivial bundle
. A locally trivial bundle 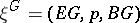 is now called universal if the mapping
is now called universal if the mapping 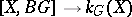 ,
, 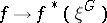 , is one-to-one (and onto) for any
, is one-to-one (and onto) for any 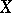 . In this case, the space
. In this case, the space 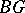 is called a classifying space of the group
is called a classifying space of the group 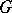 . A principal bundle with structure group
. A principal bundle with structure group 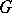 is universal (in the class of locally trivial bundles over
is universal (in the class of locally trivial bundles over 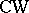 -complexes) if the space of the bundle has trivial homotopy groups.
-complexes) if the space of the bundle has trivial homotopy groups.
The most important examples of classifying spaces are 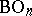 ,
, 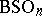 ,
, 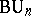 ,
, 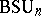 for the respective groups
for the respective groups 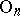 ,
, 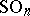 ,
, 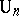 ,
, 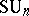 , and are constructed as follows. Let
, and are constructed as follows. Let  be the Grassmann manifold; it is the base of the principal
be the Grassmann manifold; it is the base of the principal 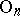 -bundle with the Stiefel manifold
-bundle with the Stiefel manifold 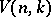 as total space. The natural imbeddings
as total space. The natural imbeddings 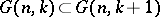 and
and  allow one to form the unions
allow one to form the unions 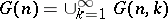 and
and 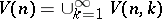 . The bundle
. The bundle 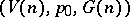 is universal and
is universal and 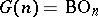 is a classifying space for the group
is a classifying space for the group 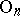 (
(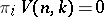 for
for 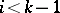 and
and 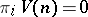 for all
for all 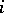 ). The Grassmann manifold
). The Grassmann manifold  (the space of
(the space of  -dimensional planes with a fixed orientation in
-dimensional planes with a fixed orientation in 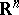 ) leads in analogous fashion to the classifying space
) leads in analogous fashion to the classifying space 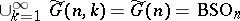 for the group
for the group 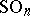 . The classifying spaces for the groups
. The classifying spaces for the groups 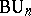 and
and 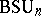 are similarly constructed, but with the difference that here complex Grassmann manifolds are considered.
are similarly constructed, but with the difference that here complex Grassmann manifolds are considered.
For any 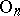 -bundle
-bundle 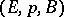 (where
(where 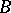 is a
is a 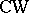 -complex) there exists a mapping
-complex) there exists a mapping  under which the induced bundle over
under which the induced bundle over 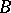 is isomorphic to
is isomorphic to 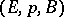 . In the case when
. In the case when 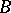 is a smooth
is a smooth  -dimensional manifold and the principal
-dimensional manifold and the principal 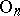 -bundle
-bundle 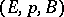 is associated with the tangent vector bundle to
is associated with the tangent vector bundle to 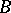 , the construction of
, the construction of  is especially simple: The manifold
is especially simple: The manifold 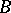 is imbedded in a Euclidean space
is imbedded in a Euclidean space 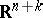 for sufficiently large
for sufficiently large 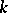 and
and  ,
, 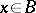 , is taken to coincide with the
, is taken to coincide with the  -dimensional subspace of
-dimensional subspace of 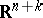 obtained by a displacement of the tangent space to
obtained by a displacement of the tangent space to 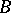 at
at  . The Grassmann manifolds provide a convenient method of constructing classifying spaces for vector bundles. There are also constructions enabling one to construct classifying spaces functorially for any topological group. The most commonly used is the Milnor construction
. The Grassmann manifolds provide a convenient method of constructing classifying spaces for vector bundles. There are also constructions enabling one to construct classifying spaces functorially for any topological group. The most commonly used is the Milnor construction 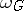 (see Principal fibre bundle) for which
(see Principal fibre bundle) for which 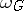 is universal in the wider category of all numerable
is universal in the wider category of all numerable 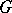 -bundles over an arbitrary topological space.
-bundles over an arbitrary topological space.
Classifying spaces play an important role for spherical bundles 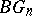 over a
over a 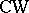 -complex
-complex 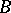 ; the Milnor construction is not suitable for the construction of the spaces
; the Milnor construction is not suitable for the construction of the spaces 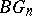 (and of
(and of 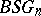 for orientable spherical bundles) since the set of homotopy equivalences
for orientable spherical bundles) since the set of homotopy equivalences 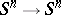 is not a group but an
is not a group but an 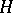 -space. An explicit construction of these spaces is given in [2]. There also exist classifying spaces
-space. An explicit construction of these spaces is given in [2]. There also exist classifying spaces 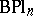 and
and 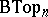 for piecewise-linear and topological microbundles.
for piecewise-linear and topological microbundles.
There is a natural mapping 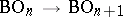 corresponding to the addition of a one-dimensional trivial bundle to a vector bundle. The mapping can be regarded as an imbedding, so that it makes sense to consider the union
corresponding to the addition of a one-dimensional trivial bundle to a vector bundle. The mapping can be regarded as an imbedding, so that it makes sense to consider the union  in the inductive limit topology. The spaces
in the inductive limit topology. The spaces 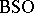 ,
, 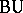 ,
, 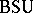 ,
, 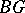 ,
, 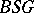 ,
, 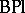 ,
, 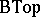 , etc., are constructed in a completely analogous fashion. These are classifying spaces for stable equivalence classes of bundles given over connected finite
, etc., are constructed in a completely analogous fashion. These are classifying spaces for stable equivalence classes of bundles given over connected finite 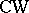 -complexes. All these spaces have
-complexes. All these spaces have 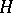 -space structures coming from the operation of Whitney sums of fibre bundles.
-space structures coming from the operation of Whitney sums of fibre bundles.
The term "classifying space" is not used solely in connection with fibre bundles. Sometimes classifying space refers to the representing space (object) for an arbitrary representable functor 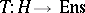 of the homotopy category into the category of sets. An example of such a classifying space is the space
of the homotopy category into the category of sets. An example of such a classifying space is the space 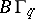 which classifies in some sense foliations (cf. Foliation) of codimension
which classifies in some sense foliations (cf. Foliation) of codimension 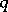 on a manifold, or, more generally, Haefliger
on a manifold, or, more generally, Haefliger 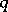 -structures on an arbitrary topological space.
-structures on an arbitrary topological space.
References
| [1] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) MR0229247 Zbl 0144.44804 |
| [2] | J.M. Boardman, R.M. Vogt, "Homotopy invariant algebraic structures on topological spaces" , Springer (1973) MR0420609 MR0420610 Zbl 0285.55012 |
Comments
Two vector bundles 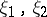 are stably equivalent (with respect to some notion of isomorphism) if there are trivial bundles
are stably equivalent (with respect to some notion of isomorphism) if there are trivial bundles 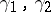 such that the Whitney sums (direct sums)
such that the Whitney sums (direct sums) 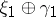 and
and 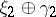 are isomorphic in the chosen sense.
are isomorphic in the chosen sense.
An open covering 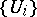 of a topological space is numerable if there exists a locally finite partition of unity
of a topological space is numerable if there exists a locally finite partition of unity  such that
such that 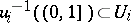 for all
for all  . A
. A 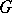 -bundle
-bundle 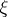 over
over 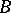 is numerable if there is a numerable covering
is numerable if there is a numerable covering 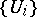 such that
such that 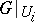 is trivial for all
is trivial for all 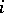 .
.
Very often in the literature  classifying space of a group is defined as the base space of a totally acyclic principal fibre bundle. One may as well (as is done above) consider the class of locally trivial fibre bundles with structure group
classifying space of a group is defined as the base space of a totally acyclic principal fibre bundle. One may as well (as is done above) consider the class of locally trivial fibre bundles with structure group 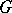 , and define a classifying space as the base space of a universal locally trivial bundle. In principle the classifying space thus defined depends then also on the special fibre type. But as it is proved in the literature (up to homotopy equivalence) the classifying spaces are independent of the fibre type.
, and define a classifying space as the base space of a universal locally trivial bundle. In principle the classifying space thus defined depends then also on the special fibre type. But as it is proved in the literature (up to homotopy equivalence) the classifying spaces are independent of the fibre type.
For more on such classifying spaces as  and
and 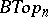 cf. [a2]. The elements of the cohomology rings of classifying spaces such as
cf. [a2]. The elements of the cohomology rings of classifying spaces such as  ,
, 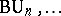 define characteristic classes (cf. Characteristic class) by assigning e.g. for a given element
define characteristic classes (cf. Characteristic class) by assigning e.g. for a given element 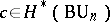 to an
to an  -dimensional complex vector bundle
-dimensional complex vector bundle 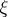 over
over 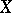 the cohomology element
the cohomology element 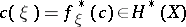 where
where 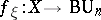 is the mapping (unique up to homotopy) such that
is the mapping (unique up to homotopy) such that 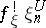 is isomorphic to
is isomorphic to 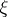 (where
(where 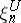 is the universal complex vector bundle over
is the universal complex vector bundle over 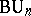 );
); 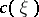 is called the characteristic cohomology class of
is called the characteristic cohomology class of 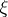 determined by
determined by  .
.
References
| [a1] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) MR0440554 Zbl 0298.57008 |
| [a2] | J. Madsen, R.J. Milgram, "The classifying spaces for surgery and cobordism of manifolds" , Princeton Univ. Press (1979) MR0548575 Zbl 0446.57002 |
Classifying space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Classifying_space&oldid=24397