Difference between revisions of "3-Sasakian manifold"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 25: | Line 25: | ||
with odd Betti numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010124.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010125.png" />. In fact the vanishing of odd Betti numbers holds true in the irregular case as well. There are, however, examples of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010126.png" />-dimensional irregular <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010127.png" />-Sasakian manifold for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010128.png" /> and of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010129.png" />-dimensional manifolds with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010130.png" />. These were constructed explicitly by C. Boyer, K. Galicki and B. Mann [[#References|[a5]]]. | with odd Betti numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010124.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010125.png" />. In fact the vanishing of odd Betti numbers holds true in the irregular case as well. There are, however, examples of an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010126.png" />-dimensional irregular <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010127.png" />-Sasakian manifold for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010128.png" /> and of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010129.png" />-dimensional manifolds with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010130.png" />. These were constructed explicitly by C. Boyer, K. Galicki and B. Mann [[#References|[a5]]]. | ||
| − | The first complete irregular examples that are not quotients of homogeneous spaces by a discrete group of isometries were obtained also by Boyer, Galicki and Mann [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a15]]], using a method called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010132.png" />-Sasakian reduction. The examples are bi-quotients of unitary groups of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010133.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010134.png" />-dimensional family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010135.png" /> depends on positive integral | + | The first complete irregular examples that are not quotients of homogeneous spaces by a discrete group of isometries were obtained also by Boyer, Galicki and Mann [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a15]]], using a method called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010132.png" />-Sasakian reduction. The examples are bi-quotients of unitary groups of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010133.png" />. The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010134.png" />-dimensional family <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010135.png" /> depends on positive integral "weights" <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010136.png" /> which are pairwise relatively prime. The integral cohomology ring of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010137.png" /> depends on the weight vector <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010138.png" /> and one gets infinitely many homotopy types of compact simply-connected <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010139.png" />-Sasakian manifolds in each allowable dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010140.png" />. Other irregular examples were constructed later in dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010141.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010142.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010143.png" /> by Boyer, Galicki, Mann, and E. Rees [[#References|[a6]]]. The same method of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010144.png" />-Sasakian reduction was used to obtain families of compact simply-connected <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010145.png" />-Sasakian <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010146.png" />-manifolds with an arbitrary second Betti number. All these examples are toric, i.e., having <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010147.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010148.png" /> as the group of isometries with the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010149.png" />-torus action preserving the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010150.png" />-Sasakian structure. R. Bielawski [[#References|[a7]]] showed that, in any dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010151.png" />, a toric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010152.png" />-Sasakian manifold is necessarily diffeomorphic to one of the quotients obtained in [[#References|[a6]]]. Examples of compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010153.png" />-Sasakian manifold which are not toric can also be constructed. |
After their introduction in 1969, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010154.png" />-Sasakian manifolds were vigorously studied by a group of Japanese geometers, including S. Ishihara, T. Kashiwada, M. Konishi, Y. Kuo, S. Tachibana, S. Tanno, and W.N. Yu [[#References|[a16]]], [[#References|[a17]]], [[#References|[a18]]], [[#References|[a19]]], [[#References|[a20]]], [[#References|[a21]]], [[#References|[a22]]], [[#References|[a23]]]. This lasted until 1975, when the whole subject was relegated to an almost complete obscurity largely due to lack of any interesting examples. In the early 1990s <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010155.png" />-Sasakian manifolds returned in two different areas. One of them is the study of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010156.png" />-manifolds admitting Killing spinors, in the work of T. Friedrich and I. Kath [[#References|[a8]]]. The other is the work [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a15]]], of Boyer–Galicki–Mann, in which the first irregular examples are constructed and a systematic study of geometry and topology of compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010157.png" />-Sasakian manifolds is undertaken. | After their introduction in 1969, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010154.png" />-Sasakian manifolds were vigorously studied by a group of Japanese geometers, including S. Ishihara, T. Kashiwada, M. Konishi, Y. Kuo, S. Tachibana, S. Tanno, and W.N. Yu [[#References|[a16]]], [[#References|[a17]]], [[#References|[a18]]], [[#References|[a19]]], [[#References|[a20]]], [[#References|[a21]]], [[#References|[a22]]], [[#References|[a23]]]. This lasted until 1975, when the whole subject was relegated to an almost complete obscurity largely due to lack of any interesting examples. In the early 1990s <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010155.png" />-Sasakian manifolds returned in two different areas. One of them is the study of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010156.png" />-manifolds admitting Killing spinors, in the work of T. Friedrich and I. Kath [[#References|[a8]]]. The other is the work [[#References|[a10]]], [[#References|[a11]]], [[#References|[a12]]], [[#References|[a13]]], [[#References|[a14]]], [[#References|[a15]]], of Boyer–Galicki–Mann, in which the first irregular examples are constructed and a systematic study of geometry and topology of compact <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010157.png" />-Sasakian manifolds is undertaken. | ||
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Udrişte, "Structures presque coquaternioniennes" ''Bull. Math. Soc. Sci. Math. Roum.'' , '''12''' (1969) pp. 487–507 {{MR|0296849}} {{ZBL|0213.48205}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> Y.-Y. Kuo, "On almost contact 3-structure" ''Tôhoku Math. J.'' , '''22''' (1970) pp. 325–332 {{MR|0278225}} {{ZBL|0205.25801}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> K. Galicki, S. Salamon, "On Betti numbers of 3-Sasakian manifolds" ''Geom. Dedicata'' , '''63''' (1996) pp. 45–68 {{MR|1413621}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> C. LeBrun, S.M. Salamon, "Strong rigidity of positive quaternion–Kähler manifolds" ''Invent. Math.'' , '''118''' (1994) pp. 109–132</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "A note on smooth toral reductions of spheres" ''Manuscripta Math.'' , '''95''' (1998) pp. 149–158 {{MR|1603301}} {{ZBL|0913.53020}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, E. Rees, "Compact 3-Sasakian 7-manifolds with arbitrary second Betti number" ''Invent. Math.'' , '''131''' (1998) pp. 321–344 {{MR|1608567}} {{ZBL|0901.53033}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> R. Bielawski, "Complete <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010158.png" />-invariant hyperkähler <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120010/t120010159.png" />-manifolds" ''MPI preprint'' , '''65''' (1998) (www.mpim-bonn.mpg.de/html/preprints/preprints.html)</TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> T. Friedrich, I. Kath, "Compact seven-dimensional manifolds with Killing spinors" ''Comm. Math. Phys.'' , '''133''' (1990) pp. 543–561</TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, "3-Sasakian Manifolds" C. LeBrun (ed.) M. Wang (ed.) , ''Essays on Einstein Manifolds'' , Internat. Press (to appear) {{MR|1798609}} {{MR|1645769}} {{MR|1433200}} {{MR|1293878}} {{MR|1249451}} {{ZBL|1008.53047}} {{ZBL|0942.53030}} {{ZBL|0901.53033}} {{ZBL|0889.53029}} {{ZBL|0814.53037}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "Quaternionic reduction and Einstein manifolds" ''Commun. Anal. Geom.'' , '''1''' (1993) pp. 1–51 {{MR|1243524}} {{ZBL|0856.53038}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "The geometry and topology of 3-Sasakian manifolds" ''J. Reine Angew. Math.'' , '''455''' (1994) pp. 183–220 {{MR|1293878}} {{ZBL|0889.53029}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" ''Math. Res. Lett.'' , '''1''' (1994) pp. 115–121 {{MR|1258497}} {{ZBL|0842.53033}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "3-Sasakian manifolds" ''Proc. Japan Acad. Ser. A'' , '''69''' (1993) pp. 335–340 {{MR|1249451}} {{ZBL|0814.53037}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "Hypercomplex structures on Stiefel manifolds" ''Ann. Global Anal. Geom.'' , '''14''' (1996) pp. 81–105 {{MR|1375068}} {{ZBL|0843.53030}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" ''Bull. London Math. Soc.'' , '''28''' (1996) pp. 401–408 {{MR|1258497}} {{ZBL|0842.53033}} </TD></TR><TR><TD valign="top">[a16]</TD> <TD valign="top"> S. Ishihara, M. Konishi, "Fibered Riemannian spaces with Sasakian 3-structure" , ''Differential Geometry, in Honor of K. Yano'' , Kinokuniya (1972) pp. 179–194</TD></TR><TR><TD valign="top">[a17]</TD> <TD valign="top"> S. Ishihara, "Quaternion Kählerian manifolds and fibered Riemannian spaces with Sasakian 3-structure" ''Kodai Math. Sem. Rep.'' , '''25''' (1973) pp. 321–329</TD></TR><TR><TD valign="top">[a18]</TD> <TD valign="top"> T. Kashiwada, "A note on a Riemannian space with Sasakian 3-structure" ''Nat. Sci. Rep. Ochanomizu Univ.'' , '''22''' (1971) pp. 1–2 {{MR|0303449}} {{ZBL|0228.53033}} </TD></TR><TR><TD valign="top">[a19]</TD> <TD valign="top"> M. Konishi, "On manifolds with Sasakian 3-structure over quaternion Kählerian manifolds" ''Kodai Math. Sem. Rep.'' , '''26''' (1975) pp. 194–200</TD></TR><TR><TD valign="top">[a20]</TD> <TD valign="top"> Y.-Y. Kuo, S. Tachibana, "On the distribution appeared in contact 3-structure" ''Taita J. Math.'' , '''2''' (1970) pp. 17–24 {{MR|0309004}} {{ZBL|0231.53053}} </TD></TR><TR><TD valign="top">[a21]</TD> <TD valign="top"> S. Tachibana, W.N. Yu, "On a Riemannian space admitting more than one Sasakian structure" ''Tôhoku Math. J.'' , '''22''' (1970) pp. 536–540 {{MR|0275329}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a22]</TD> <TD valign="top"> S. Tanno, "Killing vectors on contact Riemannian manifolds and fiberings related to the Hopf fibrations" ''Tôhoku Math. J.'' , '''23''' (1971) pp. 313–333 {{MR|0287477}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a23]</TD> <TD valign="top"> S. Tanno, "On the isometry of Sasakian manifolds" ''J. Math. Soc. Japan'' , '''22''' (1970) pp. 579–590 {{MR|271874}} {{ZBL|0197.48004}} </TD></TR></table> |
Revision as of 16:54, 15 April 2012
Sasakian and  -Sasakian spaces are odd-dimensional companions of Kähler and hyper-Kähler manifolds, respectively. A Riemannian manifold
-Sasakian spaces are odd-dimensional companions of Kähler and hyper-Kähler manifolds, respectively. A Riemannian manifold 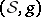 of dimension
of dimension 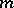 is called Sasakian if the holonomy group of the metric cone
is called Sasakian if the holonomy group of the metric cone 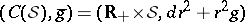 reduces to a subgroup of
reduces to a subgroup of 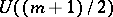 . In particular,
. In particular, 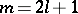 ,
, 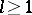 , and such a cone is a Kähler manifold. Let
, and such a cone is a Kähler manifold. Let 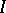 be a complex structure on
be a complex structure on 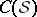 . Then
. Then 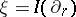 restricted to
restricted to 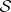 is a unit Killing vector field (cf. also Killing vector) with the property that the sectional curvature of every section containing
is a unit Killing vector field (cf. also Killing vector) with the property that the sectional curvature of every section containing 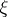 equals one. Such a
equals one. Such a 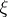 is called the characteristic vector field on
is called the characteristic vector field on 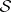 and its properties can be used as an alternative characterization of a Sasakian manifold.
and its properties can be used as an alternative characterization of a Sasakian manifold.
Similarly, one says that  is a
is a  -Sasakian manifold if the holonomy group of the metric cone
-Sasakian manifold if the holonomy group of the metric cone 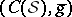 reduces to a subgroup of
reduces to a subgroup of 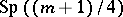 . In particular,
. In particular, 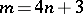 ,
, 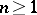 , and the cone is a hyper-Kähler manifold. When
, and the cone is a hyper-Kähler manifold. When 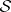 is
is  -Sasakian, the hyper-Kähler structure on the associated cone
-Sasakian, the hyper-Kähler structure on the associated cone 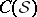 can be used to define three vector fields
can be used to define three vector fields 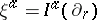 ,
, 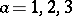 , where
, where 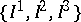 is a hypercomplex structure on
is a hypercomplex structure on 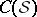 . It follows that, when restricted to
. It follows that, when restricted to 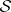 ,
, 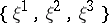 are Killing vector fields such that
are Killing vector fields such that  and
and 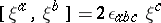 . Hence, they are orthonormal and locally define an isometric
. Hence, they are orthonormal and locally define an isometric 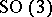 (or
(or 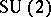 ) action on
) action on 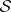 . In turn, the triple
. In turn, the triple 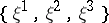 yields
yields 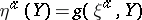 and
and  for each
for each 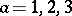 . The collection of tensors
. The collection of tensors 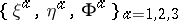 is traditionally called the
is traditionally called the  -Sasakian structure on
-Sasakian structure on 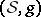 . This is the way such structures were first introduced in the work of C. Udrişte [a1] and Y. Kuo [a2] in 1969 and 1970.
. This is the way such structures were first introduced in the work of C. Udrişte [a1] and Y. Kuo [a2] in 1969 and 1970.
Every  -Sasakian manifold is an Einstein manifold with positive Einstein constant
-Sasakian manifold is an Einstein manifold with positive Einstein constant 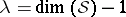 . If
. If 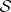 is complete, it is compact with finite fundamental group. If
is complete, it is compact with finite fundamental group. If 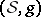 is compact, the characteristic vector fields
is compact, the characteristic vector fields 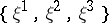 are complete and define a
are complete and define a  -dimensional foliation
-dimensional foliation 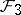 on
on 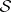 . The leaves of this foliation are necessarily compact, since
. The leaves of this foliation are necessarily compact, since  defines a locally free
defines a locally free 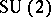 action on
action on 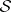 . Hence, the foliation
. Hence, the foliation 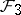 is automatically almost-regular and the space of leaves is a compact orbifold, denoted by
is automatically almost-regular and the space of leaves is a compact orbifold, denoted by 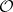 . The leaves of
. The leaves of 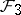 are totally geodesic submanifolds of constant sectional curvature equal one (cf. also Totally-geodesic manifold). They are all
are totally geodesic submanifolds of constant sectional curvature equal one (cf. also Totally-geodesic manifold). They are all  -dimensional homogeneous spherical space forms
-dimensional homogeneous spherical space forms 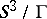 , where
, where 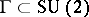 is a finite subgroup (cf. also Space forms). In particular, the leaves are
is a finite subgroup (cf. also Space forms). In particular, the leaves are  -Sasakian manifolds themselves. The space of leaves
-Sasakian manifolds themselves. The space of leaves 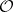 is a compact positive quaternion Kähler orbifold. The principal leaves are always diffeomorphic to either
is a compact positive quaternion Kähler orbifold. The principal leaves are always diffeomorphic to either 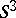 or
or 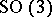 . A compact
. A compact  -Sasakian manifold is said to be regular if
-Sasakian manifold is said to be regular if 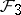 is regular, i.e., if all the leaves are diffeomorphic. In this case
is regular, i.e., if all the leaves are diffeomorphic. In this case 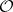 is a smooth manifold (cf. Differentiable manifold). For any
is a smooth manifold (cf. Differentiable manifold). For any  such that
such that 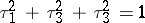 , the vector field
, the vector field  has the Sasakian property. Hence, a
has the Sasakian property. Hence, a  -Sasakian manifold has a
-Sasakian manifold has a  -sphere worth of Sasakian structures (just as hyper-Kähler manifold has an
-sphere worth of Sasakian structures (just as hyper-Kähler manifold has an 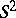 -worth of complex structures). When
-worth of complex structures). When 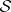 is compact, the vector field
is compact, the vector field 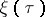 defines a
defines a 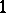 -dimensional foliation
-dimensional foliation 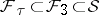 with compact leaves. Such a foliation gives
with compact leaves. Such a foliation gives 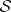 an isometric locally free circle action
an isometric locally free circle action 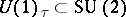 . The space of leaves
. The space of leaves 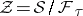 is a compact Kähler–Einstein orbifold of positive scalar curvature. It is a simply-connected normal projective algebraic variety (cf. Projective algebraic set).
is a compact Kähler–Einstein orbifold of positive scalar curvature. It is a simply-connected normal projective algebraic variety (cf. Projective algebraic set). 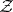 has a complex contact structure and it is a
has a complex contact structure and it is a 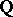 -factorial Fano variety (cf. also Fano variety). It is an orbifold twistor space of
-factorial Fano variety (cf. also Fano variety). It is an orbifold twistor space of 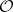 . All the foliations associated to
. All the foliations associated to 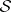 can be described in the the following diagram
can be described in the the following diagram 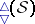 of orbifold fibrations:
of orbifold fibrations:
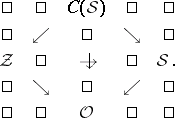 |
All four geometries in the above diagram are Einstein. Both 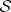 and
and  admit second, non-isometric Einstein metrics of positive scalar curvature. Every
admit second, non-isometric Einstein metrics of positive scalar curvature. Every  -Sasakian manifold is a spin manifold (cf. Spinor structure). When
-Sasakian manifold is a spin manifold (cf. Spinor structure). When 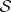 is complete, simply-connected and not of constant curvature, it admits
is complete, simply-connected and not of constant curvature, it admits 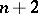 Killing spinors, where
Killing spinors, where 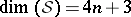 . The holonomy group of
. The holonomy group of  never reduces to a proper subgroup of
never reduces to a proper subgroup of 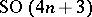 and the metric admits no infinitesimal deformations.
and the metric admits no infinitesimal deformations.
For every compact semi-simple Lie group 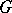 one has a corresponding diagram
one has a corresponding diagram 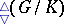 with
with 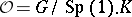 being a symmetric positive quaternion Kähler manifold (a Wolf space) and
being a symmetric positive quaternion Kähler manifold (a Wolf space) and 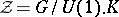 . In particular, every every
. In particular, every every  -Sasakian
-Sasakian 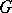 -homogeneous space is regular and it is one of the spaces
-homogeneous space is regular and it is one of the spaces
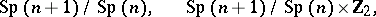 |
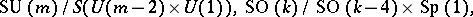 |
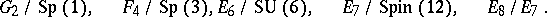 |
Here, 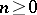 ,
,  denotes the trivial group,
denotes the trivial group, 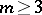 , and
, and 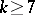 . Hence, there is one-to-one correspondence between the simple Lie algebras and the simply-connected
. Hence, there is one-to-one correspondence between the simple Lie algebras and the simply-connected  -Sasakian homogeneous manifolds.
-Sasakian homogeneous manifolds.
There is a conjecture that all complete regular  -Sasakian manifolds are homogeneous. It is a simple translation of the corresponding conjecture due to C. LeBrun and S. Salamon [a3] that all positive quaternion Kähler manifolds are symmetric. This is known to be true when
-Sasakian manifolds are homogeneous. It is a simple translation of the corresponding conjecture due to C. LeBrun and S. Salamon [a3] that all positive quaternion Kähler manifolds are symmetric. This is known to be true when 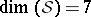 or
or 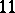 (
(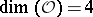 or
or 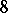 ). More generally, it is know that in each dimension
). More generally, it is know that in each dimension 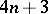 , there are only finitely many complete regular
, there are only finitely many complete regular  -Sasakian manifolds, all of them having
-Sasakian manifolds, all of them having 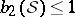 with equality holding only when
with equality holding only when 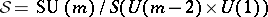 . Furthermore, it was shown by K. Galicki and S. Salamon [a4] that each Betti number of such an
. Furthermore, it was shown by K. Galicki and S. Salamon [a4] that each Betti number of such an 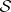 must satisfy the linear relation
must satisfy the linear relation
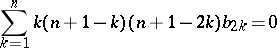 |
with odd Betti numbers 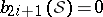 for
for 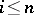 . In fact the vanishing of odd Betti numbers holds true in the irregular case as well. There are, however, examples of an
. In fact the vanishing of odd Betti numbers holds true in the irregular case as well. There are, however, examples of an  -dimensional irregular
-dimensional irregular  -Sasakian manifold for which
-Sasakian manifold for which 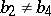 and of
and of 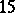 -dimensional manifolds with
-dimensional manifolds with 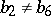 . These were constructed explicitly by C. Boyer, K. Galicki and B. Mann [a5].
. These were constructed explicitly by C. Boyer, K. Galicki and B. Mann [a5].
The first complete irregular examples that are not quotients of homogeneous spaces by a discrete group of isometries were obtained also by Boyer, Galicki and Mann [a10], [a11], [a12], [a13], [a14], [a15], using a method called  -Sasakian reduction. The examples are bi-quotients of unitary groups of the form
-Sasakian reduction. The examples are bi-quotients of unitary groups of the form 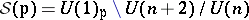 . The
. The 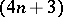 -dimensional family
-dimensional family 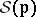 depends on positive integral "weights"
depends on positive integral "weights" 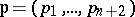 which are pairwise relatively prime. The integral cohomology ring of
which are pairwise relatively prime. The integral cohomology ring of 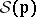 depends on the weight vector
depends on the weight vector 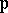 and one gets infinitely many homotopy types of compact simply-connected
and one gets infinitely many homotopy types of compact simply-connected  -Sasakian manifolds in each allowable dimension
-Sasakian manifolds in each allowable dimension  . Other irregular examples were constructed later in dimension
. Other irregular examples were constructed later in dimension 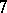 ,
, 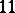 ,
, 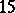 by Boyer, Galicki, Mann, and E. Rees [a6]. The same method of
by Boyer, Galicki, Mann, and E. Rees [a6]. The same method of  -Sasakian reduction was used to obtain families of compact simply-connected
-Sasakian reduction was used to obtain families of compact simply-connected  -Sasakian
-Sasakian 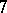 -manifolds with an arbitrary second Betti number. All these examples are toric, i.e., having
-manifolds with an arbitrary second Betti number. All these examples are toric, i.e., having  or
or 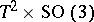 as the group of isometries with the
as the group of isometries with the  -torus action preserving the
-torus action preserving the  -Sasakian structure. R. Bielawski [a7] showed that, in any dimension
-Sasakian structure. R. Bielawski [a7] showed that, in any dimension 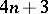 , a toric
, a toric  -Sasakian manifold is necessarily diffeomorphic to one of the quotients obtained in [a6]. Examples of compact
-Sasakian manifold is necessarily diffeomorphic to one of the quotients obtained in [a6]. Examples of compact  -Sasakian manifold which are not toric can also be constructed.
-Sasakian manifold which are not toric can also be constructed.
After their introduction in 1969,  -Sasakian manifolds were vigorously studied by a group of Japanese geometers, including S. Ishihara, T. Kashiwada, M. Konishi, Y. Kuo, S. Tachibana, S. Tanno, and W.N. Yu [a16], [a17], [a18], [a19], [a20], [a21], [a22], [a23]. This lasted until 1975, when the whole subject was relegated to an almost complete obscurity largely due to lack of any interesting examples. In the early 1990s
-Sasakian manifolds were vigorously studied by a group of Japanese geometers, including S. Ishihara, T. Kashiwada, M. Konishi, Y. Kuo, S. Tachibana, S. Tanno, and W.N. Yu [a16], [a17], [a18], [a19], [a20], [a21], [a22], [a23]. This lasted until 1975, when the whole subject was relegated to an almost complete obscurity largely due to lack of any interesting examples. In the early 1990s  -Sasakian manifolds returned in two different areas. One of them is the study of
-Sasakian manifolds returned in two different areas. One of them is the study of 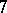 -manifolds admitting Killing spinors, in the work of T. Friedrich and I. Kath [a8]. The other is the work [a10], [a11], [a12], [a13], [a14], [a15], of Boyer–Galicki–Mann, in which the first irregular examples are constructed and a systematic study of geometry and topology of compact
-manifolds admitting Killing spinors, in the work of T. Friedrich and I. Kath [a8]. The other is the work [a10], [a11], [a12], [a13], [a14], [a15], of Boyer–Galicki–Mann, in which the first irregular examples are constructed and a systematic study of geometry and topology of compact  -Sasakian manifolds is undertaken.
-Sasakian manifolds is undertaken.
For a detailed review of the subject and extensive bibliography see [a9].
References
| [a1] | C. Udrişte, "Structures presque coquaternioniennes" Bull. Math. Soc. Sci. Math. Roum. , 12 (1969) pp. 487–507 MR0296849 Zbl 0213.48205 |
| [a2] | Y.-Y. Kuo, "On almost contact 3-structure" Tôhoku Math. J. , 22 (1970) pp. 325–332 MR0278225 Zbl 0205.25801 |
| [a3] | K. Galicki, S. Salamon, "On Betti numbers of 3-Sasakian manifolds" Geom. Dedicata , 63 (1996) pp. 45–68 MR1413621 |
| [a4] | C. LeBrun, S.M. Salamon, "Strong rigidity of positive quaternion–Kähler manifolds" Invent. Math. , 118 (1994) pp. 109–132 |
| [a5] | C.P. Boyer, K. Galicki, B.M. Mann, "A note on smooth toral reductions of spheres" Manuscripta Math. , 95 (1998) pp. 149–158 MR1603301 Zbl 0913.53020 |
| [a6] | C.P. Boyer, K. Galicki, B.M. Mann, E. Rees, "Compact 3-Sasakian 7-manifolds with arbitrary second Betti number" Invent. Math. , 131 (1998) pp. 321–344 MR1608567 Zbl 0901.53033 |
| [a7] | R. Bielawski, "Complete 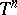 -invariant hyperkähler -invariant hyperkähler 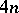 -manifolds" MPI preprint , 65 (1998) (www.mpim-bonn.mpg.de/html/preprints/preprints.html) -manifolds" MPI preprint , 65 (1998) (www.mpim-bonn.mpg.de/html/preprints/preprints.html) |
| [a8] | T. Friedrich, I. Kath, "Compact seven-dimensional manifolds with Killing spinors" Comm. Math. Phys. , 133 (1990) pp. 543–561 |
| [a9] | C.P. Boyer, K. Galicki, "3-Sasakian Manifolds" C. LeBrun (ed.) M. Wang (ed.) , Essays on Einstein Manifolds , Internat. Press (to appear) MR1798609 MR1645769 MR1433200 MR1293878 MR1249451 Zbl 1008.53047 Zbl 0942.53030 Zbl 0901.53033 Zbl 0889.53029 Zbl 0814.53037 |
| [a10] | C.P. Boyer, K. Galicki, B.M. Mann, "Quaternionic reduction and Einstein manifolds" Commun. Anal. Geom. , 1 (1993) pp. 1–51 MR1243524 Zbl 0856.53038 |
| [a11] | C.P. Boyer, K. Galicki, B.M. Mann, "The geometry and topology of 3-Sasakian manifolds" J. Reine Angew. Math. , 455 (1994) pp. 183–220 MR1293878 Zbl 0889.53029 |
| [a12] | C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" Math. Res. Lett. , 1 (1994) pp. 115–121 MR1258497 Zbl 0842.53033 |
| [a13] | C.P. Boyer, K. Galicki, B.M. Mann, "3-Sasakian manifolds" Proc. Japan Acad. Ser. A , 69 (1993) pp. 335–340 MR1249451 Zbl 0814.53037 |
| [a14] | C.P. Boyer, K. Galicki, B.M. Mann, "Hypercomplex structures on Stiefel manifolds" Ann. Global Anal. Geom. , 14 (1996) pp. 81–105 MR1375068 Zbl 0843.53030 |
| [a15] | C.P. Boyer, K. Galicki, B.M. Mann, "New examples of inhomogeneous Einstein manifolds of positive scalar curvature" Bull. London Math. Soc. , 28 (1996) pp. 401–408 MR1258497 Zbl 0842.53033 |
| [a16] | S. Ishihara, M. Konishi, "Fibered Riemannian spaces with Sasakian 3-structure" , Differential Geometry, in Honor of K. Yano , Kinokuniya (1972) pp. 179–194 |
| [a17] | S. Ishihara, "Quaternion Kählerian manifolds and fibered Riemannian spaces with Sasakian 3-structure" Kodai Math. Sem. Rep. , 25 (1973) pp. 321–329 |
| [a18] | T. Kashiwada, "A note on a Riemannian space with Sasakian 3-structure" Nat. Sci. Rep. Ochanomizu Univ. , 22 (1971) pp. 1–2 MR0303449 Zbl 0228.53033 |
| [a19] | M. Konishi, "On manifolds with Sasakian 3-structure over quaternion Kählerian manifolds" Kodai Math. Sem. Rep. , 26 (1975) pp. 194–200 |
| [a20] | Y.-Y. Kuo, S. Tachibana, "On the distribution appeared in contact 3-structure" Taita J. Math. , 2 (1970) pp. 17–24 MR0309004 Zbl 0231.53053 |
| [a21] | S. Tachibana, W.N. Yu, "On a Riemannian space admitting more than one Sasakian structure" Tôhoku Math. J. , 22 (1970) pp. 536–540 MR0275329 |
| [a22] | S. Tanno, "Killing vectors on contact Riemannian manifolds and fiberings related to the Hopf fibrations" Tôhoku Math. J. , 23 (1971) pp. 313–333 MR0287477 |
| [a23] | S. Tanno, "On the isometry of Sasakian manifolds" J. Math. Soc. Japan , 22 (1970) pp. 579–590 MR271874 Zbl 0197.48004 |
3-Sasakian manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=3-Sasakian_manifold&oldid=24357