Difference between revisions of "Zariski tangent space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Zariski, "The concept of a simple point of an abstract algebraic variety" ''Trans. Amer. Math. Soc.'' , '''62''' (1947) pp. 1–52 {{MR|0021694}} {{ZBL|0031.26101}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Samuel, "Méthodes d'algèbre abstraite en géométrie algébrique" , Springer (1955) {{MR|0072531}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> |
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
to an algebraic variety or scheme 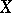 at a point
at a point 
The vector space over the residue field 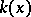 of the point
of the point  that is dual to the space
that is dual to the space 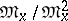 , where
, where 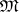 is the maximal ideal of the local ring
is the maximal ideal of the local ring 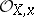 of
of  on
on 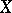 . If
. If 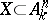 is defined by a system of equations
is defined by a system of equations
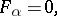 |
where 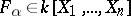 , then the Zariski tangent space at a rational point
, then the Zariski tangent space at a rational point 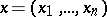 is defined by the system of linear equations
is defined by the system of linear equations
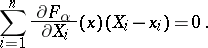 |
A variety 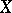 is non-singular at a rational point
is non-singular at a rational point  if and only if the dimension of the Zariski tangent space to
if and only if the dimension of the Zariski tangent space to 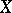 at
at  is equal to the dimension of
is equal to the dimension of 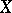 . For a rational point
. For a rational point 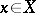 , the Zariski tangent space is dual to the space
, the Zariski tangent space is dual to the space 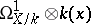 — the stalk at
— the stalk at  of the cotangent sheaf
of the cotangent sheaf 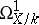 . An irreducible variety
. An irreducible variety 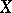 over a perfect field
over a perfect field 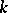 is smooth if and only if the sheaf
is smooth if and only if the sheaf 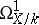 is locally free. The vector bundle
is locally free. The vector bundle 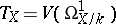 associated with
associated with 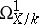 is called the tangent bundle of
is called the tangent bundle of 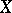 over
over 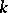 ; it is functorially related to
; it is functorially related to 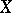 . Its sheaf of sections is called the tangent sheaf to
. Its sheaf of sections is called the tangent sheaf to 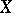 . The Zariski tangent space was introduced by O. Zariski [1].
. The Zariski tangent space was introduced by O. Zariski [1].
References
| [1] | O. Zariski, "The concept of a simple point of an abstract algebraic variety" Trans. Amer. Math. Soc. , 62 (1947) pp. 1–52 MR0021694 Zbl 0031.26101 |
| [2] | P. Samuel, "Méthodes d'algèbre abstraite en géométrie algébrique" , Springer (1955) MR0072531 |
| [3] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001 |
Zariski tangent space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zariski_tangent_space&oldid=24017