Difference between revisions of "Unirational variety"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
An algebraic variety 
over a field 
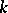into which there exists a rational mapping from a projective space, 
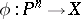, such that 
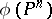is dense in 
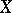and the extension of the field of rational functions 
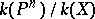is separable. In other words, 
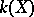has a separable extension which is purely transcendental (cf. Transcendental extension).
Unirational varieties are close to rational varieties (cf. Rational variety), e.g. on a unirational variety there are no regular differential forms,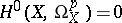 
for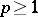 
. The problem of the coincidence of rational and unirational varieties is called the Lüroth problem; the answer is negative.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
How to Cite This Entry:
Unirational variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unirational_variety&oldid=24003
Unirational variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Unirational_variety&oldid=24003
This article was adapted from an original article by Vik.S. Kulikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article