Difference between revisions of "Trigonometric sum"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Vinogradov, , ''Selected works'' , Springer (1985) (Translated from Russian) {{MR|0807530}} {{ZBL|0577.01049}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) {{MR|0603100}} {{MR|0409380}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> I.M. Vinogradov, "Basic variants of the method of trigonometric sums" , Moscow (1976) (In Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , ''Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen'' , '''1''' : 2 , Teubner (1959) (Heft 13, Teil 1) {{MR|}} {{ZBL|0083.03601}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) {{MR|0046485}} {{ZBL|0042.07901}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> G.I. Archipov, A.A. Karatsuba, V.N. Chubarikov, "Multiple trigonometric sums" , Amer. Math. Soc. (1982) (Translated from Russian)</TD></TR></table> |
====Comments==== | ====Comments==== | ||
| − | Instead of | + | Instead of "trigonometric sum" one also uses "exponential sumexponential sum" . A complete rational exponential sum of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094250/t09425029.png" />, |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094250/t09425030.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t094/t094250/t09425030.png" /></td> </tr></table> | ||
| Line 34: | Line 34: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N.M. Korobov, "Exponential sums and their applications" , Kluwer (1992) (Translated from Russian) {{MR|1162539}} {{ZBL|0754.11022}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> N.M. Katz, "Sommes exponentielles" , Soc. Math. France (1980) {{MR|0617009}} {{ZBL|0469.12007}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N.M. Katz, "Gauss sums, Kloosterman sums, and monodromy groups" , Princeton Univ. Press (1988) {{MR|0955052}} {{ZBL|0675.14004}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
A finite sum 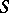 of the form
of the form
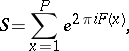 |
where 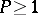 is an integer and
is an integer and 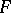 is a real-valued function of
is a real-valued function of  . More general sums
. More general sums 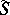 of the following form are also called trigonometric sums:
of the following form are also called trigonometric sums:
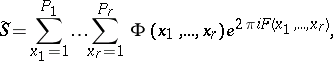 |
where  is a real-valued function and
is a real-valued function and 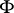 is an arbitrary complex-valued function.
is an arbitrary complex-valued function.
If 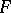 is a polynomial, then
is a polynomial, then 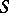 is called a Weyl sum; if the polynomial
is called a Weyl sum; if the polynomial 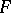 has rational coefficients,
has rational coefficients,
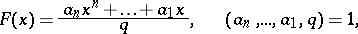 |
then 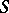 is called a rational trigonometric sum; if
is called a rational trigonometric sum; if 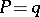 , then
, then 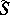 is called a complete trigonometric sum; if
is called a complete trigonometric sum; if 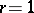 and
and 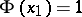 when
when 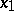 is a prime number while
is a prime number while 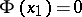 when
when 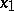 is a composite number, then
is a composite number, then  is called a trigonometric sum over prime numbers; if
is called a trigonometric sum over prime numbers; if 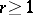 ,
, 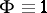 and
and  is a polynomial, then
is a polynomial, then  is called a multiple Weyl sum. A basic problem in the theory of trigonometric sums is that of finding upper bounds for the moduli of
is called a multiple Weyl sum. A basic problem in the theory of trigonometric sums is that of finding upper bounds for the moduli of 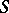 and
and 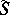 .
.
References
| [1] | I.M. Vinogradov, , Selected works , Springer (1985) (Translated from Russian) MR0807530 Zbl 0577.01049 |
| [2] | I.M. Vinogradov, "The method of trigonometric sums in the theory of numbers" , Interscience (1954) (Translated from Russian) MR0603100 MR0409380 |
| [3] | I.M. Vinogradov, "Basic variants of the method of trigonometric sums" , Moscow (1976) (In Russian) |
| [4] | L.-K. Hua, "Abschätzungen von Exponentialsummen und ihre Anwendung in der Zahlentheorie" , Enzyklopaedie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen , 1 : 2 , Teubner (1959) (Heft 13, Teil 1) Zbl 0083.03601 |
| [5] | E.C. Titchmarsh, "The theory of the Riemann zeta-function" , Clarendon Press (1951) MR0046485 Zbl 0042.07901 |
| [6] | G.I. Archipov, A.A. Karatsuba, V.N. Chubarikov, "Multiple trigonometric sums" , Amer. Math. Soc. (1982) (Translated from Russian) |
Comments
Instead of "trigonometric sum" one also uses "exponential sumexponential sum" . A complete rational exponential sum of degree  ,
,
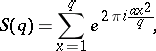 |
is called a Gauss sum. A Kloosterman sum is an exponential sum of the form
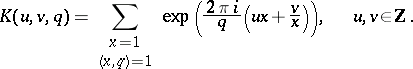 |
For these there is Weil's estimate 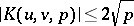 .
.
Besides in number theory (cf. also Trigonometric sums, method of), exponential sums play important roles in other fields, e.g. algebraic geometry, modular functions, quadrature formulas, monodromy, [a1], [a2], [a3].
References
| [a1] | N.M. Korobov, "Exponential sums and their applications" , Kluwer (1992) (Translated from Russian) MR1162539 Zbl 0754.11022 |
| [a2] | N.M. Katz, "Sommes exponentielles" , Soc. Math. France (1980) MR0617009 Zbl 0469.12007 |
| [a3] | N.M. Katz, "Gauss sums, Kloosterman sums, and monodromy groups" , Princeton Univ. Press (1988) MR0955052 Zbl 0675.14004 |
Trigonometric sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Trigonometric_sum&oldid=24001