Difference between revisions of "Tangent cone"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) {{MR|0346714}} {{MR|0244909}} {{ZBL|0311.53067}} </TD></TR></table> |
| Line 10: | Line 10: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , ''Contributions to geometry'' , Birkhäuser (1979) pp. 13–59 {{MR|0568493}} {{ZBL|0427.52003}} </TD></TR></table> |
The tangent cone to an algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212019.png" /> at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212020.png" /> is the set of limiting positions of the secants passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212021.png" />. More precisely, if the algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212022.png" /> is imbedded in an affine space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212023.png" /> and if it is defined by an ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212024.png" /> of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212025.png" /> so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212026.png" /> has coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212027.png" />, then the tangent cone <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212028.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212029.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212030.png" /> is given by the ideal of initial forms of the polynomials in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212031.png" />. (If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212032.png" /> is the expansion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212033.png" /> in homogeneous polynomials and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212034.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212035.png" /> is called the initial form of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212036.png" />.) There is another definition, suitable for Noetherian schemes (see [[#References|[1]]]): Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212037.png" /> be the [[Local ring|local ring]] of a [[Scheme|scheme]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212038.png" /> at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212039.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212040.png" /> be its maximal ideal. Then the spectrum of the graded ring | The tangent cone to an algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212019.png" /> at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212020.png" /> is the set of limiting positions of the secants passing through <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212021.png" />. More precisely, if the algebraic variety <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212022.png" /> is imbedded in an affine space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212023.png" /> and if it is defined by an ideal <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212024.png" /> of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212025.png" /> so that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212026.png" /> has coordinates <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212027.png" />, then the tangent cone <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212028.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212029.png" /> at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212030.png" /> is given by the ideal of initial forms of the polynomials in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212031.png" />. (If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212032.png" /> is the expansion of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212033.png" /> in homogeneous polynomials and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212034.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212035.png" /> is called the initial form of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212036.png" />.) There is another definition, suitable for Noetherian schemes (see [[#References|[1]]]): Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212037.png" /> be the [[Local ring|local ring]] of a [[Scheme|scheme]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212038.png" /> at the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212039.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092120/t09212040.png" /> be its maximal ideal. Then the spectrum of the graded ring | ||
| Line 21: | Line 21: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> J.-i. Igusa, "Normal point and tangent cone of an algebraic variety" ''Mem. Coll. Sci. Univ. Kyoto'' , '''27''' (1952) pp. 189–201 {{MR|0052155}} {{ZBL|0101.38501}} {{ZBL|0049.38504}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P. Samuel, "Méthodes d'algèbre abstraite en géométrie algébrique" , Springer (1967) {{MR|0213347}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> J. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I, II" ''Ann. of Math.'' , '''79''' (1964) pp. 109–203; 205–326 {{MR|0199184}} {{ZBL|0122.38603}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> H. Whitney, "Local properties of analytic varieties" S.S. Cairns (ed.) , ''Differential and Combinatorial Topol. (Symp. in honor of M. Morse)'' , Princeton Univ. Press (1965) pp. 205–244 {{MR|0188486}} {{ZBL|0129.39402}} </TD></TR></table> |
''V.I. Danilov'' | ''V.I. Danilov'' | ||
| Line 29: | Line 29: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
The tangent cone to a convex surface  at a point
at a point  is the surface
is the surface  of the cone formed by the half-lines emanating from
of the cone formed by the half-lines emanating from  and intersecting the convex body bounded by
and intersecting the convex body bounded by  in at least one point distinct from
in at least one point distinct from  . (This cone itself is sometimes called the solid tangent cone.) In other words,
. (This cone itself is sometimes called the solid tangent cone.) In other words,  is the boundary of the intersection of all half-spaces containing
is the boundary of the intersection of all half-spaces containing  and defined by the supporting planes to
and defined by the supporting planes to  at
at  . If
. If  is a plane, then
is a plane, then 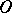 is called a smooth point of
is called a smooth point of  ; if
; if  is a dihedral angle,
is a dihedral angle,  is called a ridge point; finally, if
is called a ridge point; finally, if  is a non-degenerate (convex) cone,
is a non-degenerate (convex) cone,  is called a conic point of
is called a conic point of  .
.
References
| [1] | A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1972) (Translated from Russian) MR0346714 MR0244909 Zbl 0311.53067 |
Comments
References
| [a1] | R. Schneider, "Boundary structure and curvature of convex bodies" J. Tölke (ed.) J.M. Wills (ed.) , Contributions to geometry , Birkhäuser (1979) pp. 13–59 MR0568493 Zbl 0427.52003 |
The tangent cone to an algebraic variety 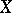 at a point
at a point  is the set of limiting positions of the secants passing through
is the set of limiting positions of the secants passing through  . More precisely, if the algebraic variety
. More precisely, if the algebraic variety 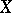 is imbedded in an affine space
is imbedded in an affine space  and if it is defined by an ideal
and if it is defined by an ideal  of the ring
of the ring 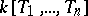 so that
so that 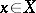 has coordinates
has coordinates 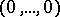 , then the tangent cone
, then the tangent cone 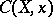 to
to  at
at  is given by the ideal of initial forms of the polynomials in
is given by the ideal of initial forms of the polynomials in  . (If
. (If 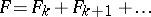 is the expansion of
is the expansion of 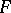 in homogeneous polynomials and
in homogeneous polynomials and 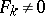 , then
, then 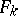 is called the initial form of
is called the initial form of 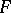 .) There is another definition, suitable for Noetherian schemes (see [1]): Let
.) There is another definition, suitable for Noetherian schemes (see [1]): Let  be the local ring of a scheme
be the local ring of a scheme 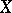 at the point
at the point  , and let
, and let 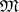 be its maximal ideal. Then the spectrum of the graded ring
be its maximal ideal. Then the spectrum of the graded ring
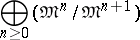 |
is called the tangent cone to 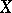 at the point
at the point  .
.
In a neighbourhood of a point  the variety
the variety 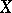 is, in a certain sense, structured in the same way as the tangent cone. For example, if the tangent cone is reduced, normal or regular, then so is the local ring
is, in a certain sense, structured in the same way as the tangent cone. For example, if the tangent cone is reduced, normal or regular, then so is the local ring  . The dimension and multiplicity of
. The dimension and multiplicity of  at
at  are the same as the dimension of the tangent cone and the multiplicity at its vertex. The tangent cone coincides with the Zariski tangent space if and only if
are the same as the dimension of the tangent cone and the multiplicity at its vertex. The tangent cone coincides with the Zariski tangent space if and only if  is a non-singular point of
is a non-singular point of 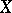 . A morphism of varieties induces a mapping of the tangent cones.
. A morphism of varieties induces a mapping of the tangent cones.
References
| [1] | J.-i. Igusa, "Normal point and tangent cone of an algebraic variety" Mem. Coll. Sci. Univ. Kyoto , 27 (1952) pp. 189–201 MR0052155 Zbl 0101.38501 Zbl 0049.38504 |
| [2] | P. Samuel, "Méthodes d'algèbre abstraite en géométrie algébrique" , Springer (1967) MR0213347 |
| [3] | J. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero I, II" Ann. of Math. , 79 (1964) pp. 109–203; 205–326 MR0199184 Zbl 0122.38603 |
| [4] | H. Whitney, "Local properties of analytic varieties" S.S. Cairns (ed.) , Differential and Combinatorial Topol. (Symp. in honor of M. Morse) , Princeton Univ. Press (1965) pp. 205–244 MR0188486 Zbl 0129.39402 |
V.I. Danilov
Comments
References
| [a1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Tangent cone. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tangent_cone&oldid=23989