Difference between revisions of "Stratification"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====Comments==== | ====Comments==== | ||
| − | Usually a | + | Usually a "stratification" of a space means more than just some decomposition into connected pieces with diminishing dimensions. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904301.png" /> be a partially ordered set. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904303.png" />-decomposition of a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904304.png" /> is a locally finite collection of subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904305.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904306.png" />, labelled by the elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904307.png" />, such that: | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904301.png" /> be a partially ordered set. A <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904303.png" />-decomposition of a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904304.png" /> is a locally finite collection of subspaces <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904305.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904306.png" />, labelled by the elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s090/s090430/s0904307.png" />, such that: | ||
| Line 31: | Line 31: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J. Mather, "Notes on topological stability" , Harvard Univ. Press (1970) (Mimeographed notes)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> C.G. Gibson, K. Wirthmüller, A.A. du Plessis, E.J.N. Looijenga, "Topological stability of smooth mappings" , ''Lect. notes in math.'' , '''552''' , Springer (1976) {{MR|0436203}} {{ZBL|0377.58006}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> M. Goresky, "Stratified Morse theory" , Springer (1988) {{MR|0932724}} {{ZBL|0639.14012}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> F. Johnson, "On the triangulation of stratified sets and singular varieties" ''Trans. Amer. Math. Soc.'' , '''275''' (1983) pp. 333–343 {{MR|0678354}} {{ZBL|0511.58007}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H. Hironaka, "Subanalytic sets" , ''Number theory, algebraic geometry and commutative algebra'' , Kinokuniya (1973) pp. 453–493 {{MR|0377101}} {{ZBL|0297.32008}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> H. Whitney, "Tangents to an analytic variety" ''Ann. of Math.'' , '''81''' (1965) pp. 496–549 {{MR|0192520}} {{ZBL|0152.27701}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H. Whitney, "Local properties of analytic varieties" S. Cairns (ed.) , ''Differentiable and Combinatorial Topology'' , Princeton Univ. Press (1965) pp. 205–244 {{MR|0188486}} {{ZBL|0129.39402}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> R. Thom, "Propriétés différentielles locales des ensembles analytiques" , ''Sem. Bourbaki'' , '''Exp. 281''' (1964/5) {{MR|1608789}} {{ZBL|0184.31402}} </TD></TR></table> |
Revision as of 21:56, 30 March 2012
A decomposition of a (possibly infinite-dimensional) manifold into connected submanifolds of strictly-diminishing dimensions.
Comments
Usually a "stratification" of a space means more than just some decomposition into connected pieces with diminishing dimensions.
Let 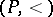 be a partially ordered set. A
be a partially ordered set. A 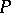 -decomposition of a topological space
-decomposition of a topological space 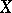 is a locally finite collection of subspaces
is a locally finite collection of subspaces 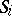 of
of 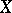 , labelled by the elements of
, labelled by the elements of 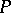 , such that:
, such that:
1) 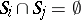 if
if 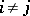 ;
;
2) 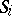 is locally closed for all
is locally closed for all 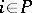 ;
;
3) 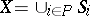 ;
;
4) if 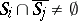 , then
, then 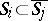 (and this is equivalent to
(and this is equivalent to 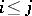 in
in 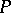 ).
).
As an example, consider the subset of 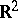 given by the inequality
given by the inequality 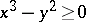 divided into the four pieces
divided into the four pieces 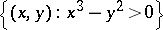 ,
, 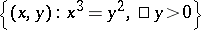 ,
, 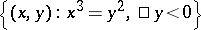 ,
, 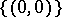 .
.
Now let 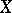 be a subset of a smooth manifold
be a subset of a smooth manifold 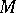 . A stratification of
. A stratification of 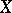 is a
is a 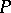 -decomposition
-decomposition 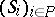 for some partially ordered set
for some partially ordered set 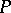 such that each of the pieces is a smooth submanifold of
such that each of the pieces is a smooth submanifold of 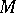 .
.
The stratification 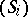 is called a Whitney stratification if for every pair of strata
is called a Whitney stratification if for every pair of strata 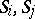 with
with 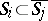 the following Whitney's conditions
the following Whitney's conditions 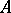 and
and 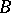 hold. Suppose that a sequence of points
hold. Suppose that a sequence of points 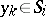 converges to
converges to 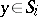 and a sequence of points
and a sequence of points 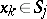 also converges to
also converges to  . Suppose, moreover, that the tangent planes
. Suppose, moreover, that the tangent planes 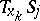 converge to some limiting plane
converge to some limiting plane 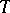 and that the secant lines
and that the secant lines 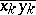 converge to some line
converge to some line 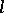 (all with respect to some local coordinate system around
(all with respect to some local coordinate system around 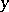 in the ambient manifold
in the ambient manifold  ). Then
). Then
A) 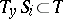 ;
;
B) 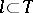 .
.
Condition B) implies in fact condition A).
A few facts and theorems concerning Whitney stratifications are as follows. Any closed subanalytic subset of an analytic manifold admits a Whitney stratification, [a5]. In particular, algebraic sets in 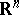 , i.e. sets given by the vanishing of finitely many polynomials (cf. also Semi-algebraic set), can be Whitney stratified. Whitney stratified spaces can be triangulated, [a4].
, i.e. sets given by the vanishing of finitely many polynomials (cf. also Semi-algebraic set), can be Whitney stratified. Whitney stratified spaces can be triangulated, [a4].
References
| [a1] | J. Mather, "Notes on topological stability" , Harvard Univ. Press (1970) (Mimeographed notes) |
| [a2] | C.G. Gibson, K. Wirthmüller, A.A. du Plessis, E.J.N. Looijenga, "Topological stability of smooth mappings" , Lect. notes in math. , 552 , Springer (1976) MR0436203 Zbl 0377.58006 |
| [a3] | M. Goresky, "Stratified Morse theory" , Springer (1988) MR0932724 Zbl 0639.14012 |
| [a4] | F. Johnson, "On the triangulation of stratified sets and singular varieties" Trans. Amer. Math. Soc. , 275 (1983) pp. 333–343 MR0678354 Zbl 0511.58007 |
| [a5] | H. Hironaka, "Subanalytic sets" , Number theory, algebraic geometry and commutative algebra , Kinokuniya (1973) pp. 453–493 MR0377101 Zbl 0297.32008 |
| [a6] | H. Whitney, "Tangents to an analytic variety" Ann. of Math. , 81 (1965) pp. 496–549 MR0192520 Zbl 0152.27701 |
| [a7] | H. Whitney, "Local properties of analytic varieties" S. Cairns (ed.) , Differentiable and Combinatorial Topology , Princeton Univ. Press (1965) pp. 205–244 MR0188486 Zbl 0129.39402 |
| [a8] | R. Thom, "Propriétés différentielles locales des ensembles analytiques" , Sem. Bourbaki , Exp. 281 (1964/5) MR1608789 Zbl 0184.31402 |
Stratification. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stratification&oldid=23983