Difference between revisions of "Separable mapping"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 8: | Line 8: | ||
A morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448029.png" /> of algebraic varieties or schemes is called dominant if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448030.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448031.png" />. | A morphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448029.png" /> of algebraic varieties or schemes is called dominant if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448030.png" /> is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448031.png" />. | ||
| − | In the Russian literature the phrase | + | In the Russian literature the phrase "separabel'noe otobrazhenie" which literally translates as "separable mapping" is sometimes encountered in the meaning "separated mapping" . |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448032.png" /> be the affine plane, and put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448033.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448034.png" /> be obtained by glueing two copies of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448035.png" /> along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448036.png" /> by the identity. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448037.png" /> is a non-separated scheme. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448032.png" /> be the affine plane, and put <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448033.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448034.png" /> be obtained by glueing two copies of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448035.png" /> along <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448036.png" /> by the identity. Then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/s/s084/s084480/s08448037.png" /> is a non-separated scheme. | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:56, 30 March 2012
A dominant morphism  between irreducible algebraic varieties
between irreducible algebraic varieties 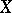 and
and 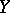 ,
, 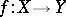 , for which the field
, for which the field 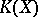 is a separable extension of the subfield
is a separable extension of the subfield  (isomorphic to
(isomorphic to  in view of the dominance). Non-separable mappings exist only when the characteristic
in view of the dominance). Non-separable mappings exist only when the characteristic 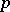 of the ground field is larger than 0. If
of the ground field is larger than 0. If 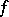 is a finite dominant morphism and its degree is not divisible by
is a finite dominant morphism and its degree is not divisible by 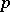 , then it is separable. For a separable mapping there exists a non-empty open set
, then it is separable. For a separable mapping there exists a non-empty open set 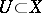 such that for all
such that for all 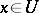 the differential
the differential 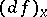 of
of 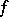 surjectively maps the tangent space
surjectively maps the tangent space 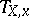 into
into 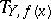 , and conversely: If the points
, and conversely: If the points  and
and 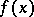 are non-singular and
are non-singular and 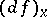 is surjective, then
is surjective, then 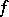 is a separable mapping.
is a separable mapping.
A morphism 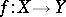 of schemes
of schemes 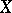 and
and 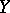 is called separated if the diagonal in
is called separated if the diagonal in 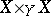 is closed. A composite of separated morphisms is separated;
is closed. A composite of separated morphisms is separated; 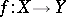 is separated if and only if for any point
is separated if and only if for any point 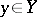 there is a neighbourhood
there is a neighbourhood 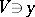 such that the morphism
such that the morphism 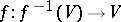 is separated. A morphism of affine schemes is always separated. There are conditions for Noetherian schemes to be separated.
is separated. A morphism of affine schemes is always separated. There are conditions for Noetherian schemes to be separated.
Comments
A morphism 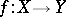 of algebraic varieties or schemes is called dominant if
of algebraic varieties or schemes is called dominant if 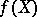 is dense in
is dense in 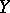 .
.
In the Russian literature the phrase "separabel'noe otobrazhenie" which literally translates as "separable mapping" is sometimes encountered in the meaning "separated mapping" .
Let 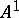 be the affine plane, and put
be the affine plane, and put 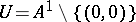 . Let
. Let  be obtained by glueing two copies of
be obtained by glueing two copies of 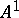 along
along 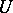 by the identity. Then
by the identity. Then 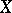 is a non-separated scheme.
is a non-separated scheme.
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001 |
Separable mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Separable_mapping&oldid=23975