Difference between revisions of "Projective algebraic set"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> O. Zariski, P. Samuel, "Commutative algebra" , '''1''' , Springer (1975) {{MR|0389876}} {{MR|0384768}} {{ZBL|0313.13001}} </TD></TR></table> |
| Line 34: | Line 34: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> D. Mumford, "Algebraic geometry" , '''1. Complex projective varieties''' , Springer (1976) {{MR|0453732}} {{ZBL|0356.14002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:55, 30 March 2012
A subset of points of a projective space  defined over a field
defined over a field  that has (in homogeneous coordinates) the form
that has (in homogeneous coordinates) the form
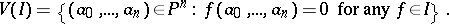 |
Here  is a homogeneous ideal in the polynomial ring
is a homogeneous ideal in the polynomial ring  . (An ideal
. (An ideal  is homogeneous if
is homogeneous if  and
and  , where the
, where the  are homogeneous polynomials of degree
are homogeneous polynomials of degree 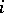 , imply that
, imply that 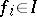 .)
.)
Projective algebraic sets possess the following properties:
1) 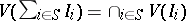 ;
;
2) 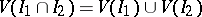 ;
;
3) if 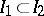 , then
, then 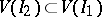 ;
;
4) 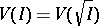 , where
, where 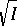 is the radical of the ideal
is the radical of the ideal 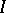 (cf. Radical of an ideal).
(cf. Radical of an ideal).
It follows from properties 1)–3) that on 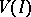 the Zariski topology can be introduced. If
the Zariski topology can be introduced. If 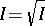 , then
, then  can be uniquely represented as the intersection of homogeneous prime ideals:
can be uniquely represented as the intersection of homogeneous prime ideals:
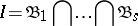 |
and
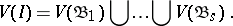 |
In the case where 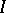 is a homogeneous prime ideal, the projective algebraic set
is a homogeneous prime ideal, the projective algebraic set 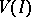 is called a projective variety.
is called a projective variety.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
| [2] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) MR0389876 MR0384768 Zbl 0313.13001 |
Comments
References
| [a1] | D. Mumford, "Algebraic geometry" , 1. Complex projective varieties , Springer (1976) MR0453732 Zbl 0356.14002 |
| [a2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 MR0463157 Zbl 0367.14001 |
Projective algebraic set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Projective_algebraic_set&oldid=23932