Difference between revisions of "Multiplicity of a singular point"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> D. Mumford, "Algebraic geometry" , '''1. Complex projective varieties''' , Springer (1976) {{MR|0453732}} {{ZBL|0356.14002}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "Algèbre locale. Multiplicités" , ''Lect. notes in math.'' , '''11''' , Springer (1965) {{MR|0201468}} {{ZBL|0142.28603}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C.P. Ramanujam, "On a geometric interpretation of multiplicity" ''Invent. Math.'' , '''22''' : 1 (1973) pp. 63–67 {{MR|0354663}} {{ZBL|0265.14004}} </TD></TR></table> |
Revision as of 21:54, 30 March 2012
of an algebraic variety
An integer which is a measure of the singularity of the algebraic variety at that point. The multiplicity 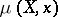 of a variety
of a variety 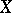 at a point
at a point  is defined to be the multiplicity of the maximal ideal
is defined to be the multiplicity of the maximal ideal 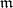 in the local ring
in the local ring 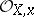 . The multiplicity of
. The multiplicity of 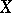 at
at  coincides with the multiplicity of the tangent cone
coincides with the multiplicity of the tangent cone 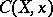 at the vertex, and also with the degree of the special fibre
at the vertex, and also with the degree of the special fibre 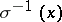 of a blow-up
of a blow-up 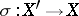 of
of 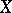 at
at  , where
, where 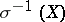 is considered to be immersed in the projective space
is considered to be immersed in the projective space  (see [3]). One has
(see [3]). One has 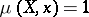 if and only if
if and only if  is a non-singular (regular) point of
is a non-singular (regular) point of 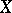 . If
. If 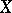 is a hypersurface in a neighbourhood of
is a hypersurface in a neighbourhood of  (i.e.
(i.e. 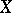 is given by a single equation
is given by a single equation 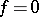 in an affine space
in an affine space 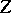 ), then
), then 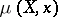 is identical with the number
is identical with the number  such that
such that 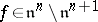 , where
, where  is the maximal ideal in the local ring
is the maximal ideal in the local ring 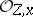 . The multiplicity does not change when
. The multiplicity does not change when 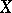 is cut by a generic hypersurface through
is cut by a generic hypersurface through  . If
. If 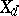 denotes the set of points
denotes the set of points 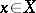 such that
such that 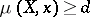 , then
, then 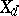 is a closed subset (a subvariety).
is a closed subset (a subvariety).
References
| [1] | D. Mumford, "Algebraic geometry" , 1. Complex projective varieties , Springer (1976) MR0453732 Zbl 0356.14002 |
| [2] | J.-P. Serre, "Algèbre locale. Multiplicités" , Lect. notes in math. , 11 , Springer (1965) MR0201468 Zbl 0142.28603 |
| [3] | C.P. Ramanujam, "On a geometric interpretation of multiplicity" Invent. Math. , 22 : 1 (1973) pp. 63–67 MR0354663 Zbl 0265.14004 |
Comments
For the multiplicity of the maximal ideal of a local ring, cf. Multiplicity of a module.
Multiplicity of a singular point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multiplicity_of_a_singular_point&oldid=23908