Difference between revisions of "Local uniformization"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 2: | Line 2: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Zariski, "Local uniformization on algebraic varieties" ''Ann. of Math. (2)'' , '''41''' (1940) pp. 852–896 {{MR|0002864}} {{ZBL|0025.21601}} {{ZBL|66.1327.02}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.S. Abhyankar, "Resolution of singularities of arithmetic surfaces" , Acad. Press (1966)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , '''3''' , Cambridge Univ. Press (1954) {{MR|0061846}} {{ZBL|0055.38705}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> O. Zariski, P. Samuel, "Commutative algebra" , '''2''' , Springer (1975) {{MR|0389876}} {{MR|0384768}} {{ZBL|0313.13001}} </TD></TR></table> |
| Line 12: | Line 12: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero" ''Ann. of Math.'' , '''79''' (1964) pp. 109–326 {{MR|0199184}} {{ZBL|0122.38603}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> S.S. Abhyankar, "Resolution of singularities of arithmetic surfaces" , Harper & Row (1965) {{MR|200272}} {{ZBL|}} </TD></TR></table> |
Revision as of 21:54, 30 March 2012
For a local ring, this is the determination of a regular local ring birationally equivalent to it. For an irreducible algebraic variety (cf. Irreducible variety) 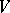 over a field
over a field 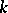 a resolving system is a family of irreducible projective varieties
a resolving system is a family of irreducible projective varieties  birationally equivalent to
birationally equivalent to 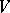 (that is, such that the rational function fields
(that is, such that the rational function fields 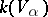 and
and 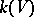 are isomorphic) and satisfying the following condition: For any valuation (place)
are isomorphic) and satisfying the following condition: For any valuation (place)  of
of 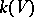 there is a variety
there is a variety 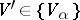 such that the centre
such that the centre 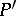 of
of  on
on 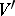 is a non-singular point. The existence of a resolving system (the local uniformization theorem) was proved for arbitrary varieties over a field of characteristic zero (see [1]), and also for two-dimensional varieties over any field and three-dimensional varieties over an algebraically closed field of characteristic other than 2, 3 or 5 (see [2]). The existence of a resolving system for
is a non-singular point. The existence of a resolving system (the local uniformization theorem) was proved for arbitrary varieties over a field of characteristic zero (see [1]), and also for two-dimensional varieties over any field and three-dimensional varieties over an algebraically closed field of characteristic other than 2, 3 or 5 (see [2]). The existence of a resolving system for 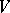 consisting of a single variety implies resolution of the singularities of
consisting of a single variety implies resolution of the singularities of 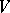 and can be obtained from the local uniformization theorem in dimension
and can be obtained from the local uniformization theorem in dimension 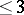 . In the general case the local uniformization theorem implies the existence of a finite resolving system (see [3]).
. In the general case the local uniformization theorem implies the existence of a finite resolving system (see [3]).
References
| [1] | O. Zariski, "Local uniformization on algebraic varieties" Ann. of Math. (2) , 41 (1940) pp. 852–896 MR0002864 Zbl 0025.21601 Zbl 66.1327.02 |
| [2] | S.S. Abhyankar, "Resolution of singularities of arithmetic surfaces" , Acad. Press (1966) |
| [3] | W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 3 , Cambridge Univ. Press (1954) MR0061846 Zbl 0055.38705 |
| [4] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , Springer (1975) MR0389876 MR0384768 Zbl 0313.13001 |
Comments
The resolution of singularities for algebraic varieties of arbitrary dimension over an algebraically closed field of characteristic zero has been achieved by H. Hironaka in 1964 [a1]. Over algebraically closed fields of characteristic 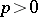 resolution of singularities for varieties of dimension 2, and for varieties of dimension 3 provided
resolution of singularities for varieties of dimension 2, and for varieties of dimension 3 provided 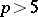 , has been proved by S.S. Abhyankar [a2].
, has been proved by S.S. Abhyankar [a2].
For (local) uniformization in analytic geometry and in the theory of functions of a complex variable (Riemann surfaces) cf. Uniformization.
References
| [a1] | H. Hironaka, "Resolution of singularities of an algebraic variety over a field of characteristic zero" Ann. of Math. , 79 (1964) pp. 109–326 MR0199184 Zbl 0122.38603 |
| [a2] | S.S. Abhyankar, "Resolution of singularities of arithmetic surfaces" , Harper & Row (1965) MR200272 |
Local uniformization. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_uniformization&oldid=23892