Difference between revisions of "Flabby sheaf"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 17: | Line 17: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) {{MR|0559531}} {{ZBL|0433.14012}} </TD></TR></table> |
Revision as of 21:52, 30 March 2012
A sheaf  of sets over a topological space
of sets over a topological space  such that for any set
such that for any set  open in
open in  the restriction mapping
the restriction mapping  is surjective. Examples of such sheaves include the sheaf of germs of all (not necessarily continuous) sections of a fibre space with base
is surjective. Examples of such sheaves include the sheaf of germs of all (not necessarily continuous) sections of a fibre space with base  , the sheaf of germs of divisors (cf. Divisor), and a prime sheaf
, the sheaf of germs of divisors (cf. Divisor), and a prime sheaf  over an irreducible algebraic variety. Flabbiness of a sheaf
over an irreducible algebraic variety. Flabbiness of a sheaf  is a local property (i.e. a flabby sheaf induces a flabby sheaf on any open set). A quotient sheaf of a flabby sheaf by a flabby sheaf is itself a flabby sheaf. The image of a flabby sheaf under a continuous mapping is a flabby sheaf. If
is a local property (i.e. a flabby sheaf induces a flabby sheaf on any open set). A quotient sheaf of a flabby sheaf by a flabby sheaf is itself a flabby sheaf. The image of a flabby sheaf under a continuous mapping is a flabby sheaf. If  is paracompact, a flabby sheaf is a soft sheaf, i.e. any section of
is paracompact, a flabby sheaf is a soft sheaf, i.e. any section of 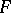 over a closed set can be extended to the entire space
over a closed set can be extended to the entire space 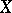 .
.
Let
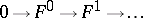 |
be an exact sequence of flabby sheaves of Abelian groups. Then, for any family 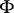 of supports, the corresponding sequence of sections (the supports of which belong to
of supports, the corresponding sequence of sections (the supports of which belong to 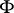 )
)
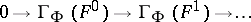 |
is exact, i.e. 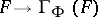 is a left-exact functor.
is a left-exact functor.
Comments
Flabby sheaves are used for resolutions in the construction of sheaf cohomology (i.e. cohomology with values in a sheaf) in algebraic geometry and topology, [a1].
References
| [a1] | J.S. Milne, "Etale cohomology" , Princeton Univ. Press (1980) MR0559531 Zbl 0433.14012 |
Flabby sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Flabby_sheaf&oldid=23831