Difference between revisions of "Cusp"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 7: | Line 7: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> W. Fulton, "Algebraic curves. An introduction to algebraic geometry" , Benjamin (1969) pp. 66 {{MR|0313252}} {{ZBL|0681.14011}} </TD></TR></table> |
Revision as of 21:51, 30 March 2012
ordinary cusp
A singular point of specific type of an algebraic curve. Namely, a singular point 
of an algebraic curve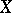 
over an algebraically closed field 
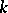is called a cusp if the completion of its local ring 
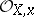is isomorphic to the completion of the local ring of the plane algebraic curve 
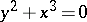at the origin.
Comments
A cusp can also be defined via the so-called intersection number of two plane curves at a point, cf. [a1], pp. 74-82. A generalization of a cusp is a hypercusp, cf. [a1], p. 82.
References
| [a1] | W. Fulton, "Algebraic curves. An introduction to algebraic geometry" , Benjamin (1969) pp. 66 MR0313252 Zbl 0681.14011 |
How to Cite This Entry:
Cusp. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cusp&oldid=23804
Cusp. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cusp&oldid=23804