Coherent sheaf

on a ringed space

A sheaf of modules over a sheaf of rings with the following properties: 1) is a sheaf of finite type, that is, it is locally generated over by a finite number of sections; and 2) the kernel of any homomorphism of sheaves of modules over an open set is a sheaf of finite type. If in an exact sequence of sheaves of -modules two of the three sheaves 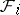are coherent, then the third is coherent as well. If is a homomorphism of coherent sheaves of 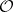-modules, then 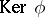, , 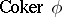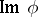are also coherent sheaves. If 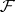and 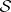are coherent, then so are and [4].

A structure sheaf is called a coherent sheaf of rings if 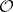is coherent as a sheaf of modules over itself, which reduces to condition 2). If is a coherent sheaf of rings, then a sheaf of 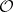-modules 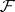is coherent if and only if every point of the space 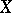has a neighbourhood 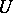over which there is an exact sequence of sheaves of 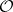-modules:

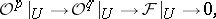[4]. Furthermore, under this condition 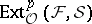is coherent for any coherent sheaves , and for all 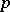(see [2]).

The fundamental classes of ringed spaces with a coherent structure sheaf are: analytic spaces over algebraically closed fields [1], Noetherian schemes and, in particular, algebraic varieties [4]. A classical special case is the sheaf of germs of holomorphic functions in a domain of 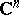; the statement that it is coherent is known as the Oka coherence theorem [3], [5]. The structure sheaf of a real-analytic space is not coherent, in general.

See also Coherent analytic sheaf; Coherent algebraic sheaf.

References

[1]	S.S. Abhyankar, "Local analytic geometry" , Acad. Press (1964) MR0175897 Zbl 0205.50401
[2]	C. Banica, O. Stanasila, "Algebraic methods in the global theory of complex spaces" , Wiley (1976) (Translated from Rumanian) MR0463470 Zbl 0334.32001
[3]	R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) MR0180696 Zbl 0141.08601
[4]	J.-P. Serre, "Faisceaux algébriques cohérents" Ann. of Math. , 61 (1955) pp. 197–278 MR0068874 Zbl 0067.16201
[5]	B.A. Fuks, "Special chapters in the theory of analytic functions of several complex variables" , Amer. Math. Soc. (1965) (Translated from Russian) MR0188477 Zbl 0146.30802