Difference between revisions of "Closed category"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 20: | Line 20: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> M. Bunge, ''Matematika'' , '''16''' : 2 (1972) pp. 11–46 {{MR|0360082}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> F.W. Lawvere, "Introduction" F.W. Lawvere (ed.) , ''Toposes, algebraic geometry and logic (Dalhousic Univ., Jan. 1971)'' , ''Lect. notes in math.'' , '''274''' , Springer (1972) {{MR|0376798}} {{ZBL|0249.18015}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.J. Dubuc, "Kan extensions in enriched category theory" , Springer (1970) {{MR|0280560}} {{ZBL|0228.18002}} </TD></TR></table> |
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 {{MR|}} {{ZBL|0232.18001}} </TD></TR></table> |
Revision as of 21:50, 30 March 2012
A category with an additional structure, thanks to which the internal Hom-functor can be used as a right-adjoint functor to the abstract tensor product.
A category  is said to be closed if a bifunctor
is said to be closed if a bifunctor 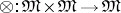 (see Functor) and a distinguished object
(see Functor) and a distinguished object 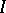 have been given on it, and if it admits natural isomorphisms
have been given on it, and if it admits natural isomorphisms
 |
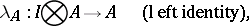 |
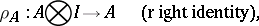 |
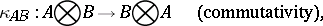 |
such that the following conditions are satisfied: 1) the natural isomorphisms 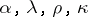 are coherent; and 2) every functor
are coherent; and 2) every functor
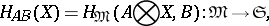 |
where 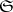 is the category of sets, is representable. The representing objects are usually denoted by
is the category of sets, is representable. The representing objects are usually denoted by 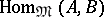 , and they can be regarded as the values of the bifunctor
, and they can be regarded as the values of the bifunctor 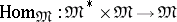 (the internal Hom-functor) on objects. If the bifunctor
(the internal Hom-functor) on objects. If the bifunctor 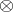 coincides with a product and
coincides with a product and  is a right zero (terminal object) of
is a right zero (terminal object) of 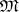 , then
, then 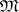 is called a Cartesian-closed category.
is called a Cartesian-closed category.
The following categories are Cartesian closed: the category of sets, the category of small categories and the category of sheaves of sets over a topological space. The following categories are closed: the category of modules over a commutative ring with an identity and the category of real (or complex) Banach spaces and linear mappings with norm not exceeding one.
References
| [1] | M. Bunge, Matematika , 16 : 2 (1972) pp. 11–46 MR0360082 |
| [2] | F.W. Lawvere, "Introduction" F.W. Lawvere (ed.) , Toposes, algebraic geometry and logic (Dalhousic Univ., Jan. 1971) , Lect. notes in math. , 274 , Springer (1972) MR0376798 Zbl 0249.18015 |
| [3] | E.J. Dubuc, "Kan extensions in enriched category theory" , Springer (1970) MR0280560 Zbl 0228.18002 |
Comments
References
| [a1] | S. MacLane, "Categories for the working mathematician" , Springer (1971) pp. Chapt. IV, Sect. 6; Chapt. VII, Sect. 7 Zbl 0232.18001 |
Closed category. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Closed_category&oldid=23785