Bertini theorems

Two theorems concerning the properties of linear systems (cf. Linear system) on algebraic varieties, due to E. Bertini [1].

Let be an algebraic variety over an algebraically closed field of characteristic 0, let be a linear system without fixed components on and let be the image of the variety under the mapping given by . The following two theorems are known as the first and the second Bertini theorem, respectively.

1) If , then almost all the divisors of the linear system (i.e. all except a closed subset in the parameter space 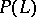not equal to 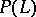) are irreducible reduced algebraic varieties.

2) Almost all divisors of 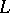have no singular points outside the basis points of the linear system 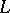and the singular points of the variety .

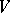Both Bertini theorems are invalid if the characteristic of the field is non-zero.

Conditions under which Bertini's theorems are valid for the case of a finite characteristic of the field have been studied [3], [6]. If 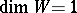, Bertini's theorem is replaced by the following theorem: Almost all fibres of the mapping are irreducible and reduced if the function field 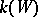is algebraically closed in the field 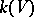under the imbedding 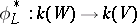. If the characteristic of 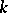is finite, the corresponding theorem is true if the extension 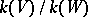is separable [3], [6]. The Bertini theorems apply to linear systems of hyperplane sections, without restrictions on the characteristic of the field [5].

References

[1]	E. Bertini, "Introduction to the projective geometry of hyperspaces" , Messina (1923) (In Italian)
[2]	"Algebraic surfaces" Trudy Mat. Inst. Steklov. , 75 (1965) (In Russian) Zbl 0154.33002 Zbl 0154.21001
[3]	M. Baldassarri, "Algebraic varieties" , Springer (1956) MR0082172 Zbl 0995.14003 Zbl 0075.15902
[4]	Y. Akizuki, "Theorems of Bertini on linear systems" J. Math. Soc. Japan , 3 : 1 (1951) pp. 170–180 MR0044160 Zbl 0043.36302
[5]	Y. Nakai, "Note on the intersection of an algebraic variety with the generic hyperplane" Mem. Coll. Sci. Univ. Kyoto Ser. A Math. , 26 : 2 (1950) pp. 185–187 MR0044161 Zbl 0045.42001
[6]	O. Zariski, "The theorem of Bertini on the variable singular points of a linear system of varieties" Trans. Amer. Math. Soc. , 56 (1944) pp. 130–140 MR0011572 Zbl 0061.33101
[7]	R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001