Difference between revisions of "Stochastic indistinguishability"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) {{MR|0448504}} {{ZBL|0246.60032}} </TD></TR></table> |
| Line 14: | Line 14: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> C. Dellacherie, P.A. Meyer, "Probabilities and potential" , '''A''' , North-Holland (1978) (Translated from French) {{MR|0521810}} {{ZBL|0494.60001}} </TD></TR></table> |
Revision as of 10:32, 27 March 2012
A property of two random processes 
and 
which states that the random set
 |
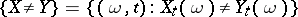can be disregarded, i.e. that the probability of the set 
is equal to zero. If 
and 
are stochastically indistinguishable, then 
for all 
, i.e. 
and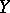 
are stochastically equivalent (cf. Stochastic equivalence). The opposite, generally speaking, is not true, but for processes that are continuous from the right (left), stochastic indistinguishability follows from stochastic equivalence.
References
| [1] | C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) MR0448504 Zbl 0246.60032 |
Comments
References
| [a1] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A , North-Holland (1978) (Translated from French) MR0521810 Zbl 0494.60001 |
How to Cite This Entry:
Stochastic indistinguishability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_indistinguishability&oldid=23661
Stochastic indistinguishability. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_indistinguishability&oldid=23661
This article was adapted from an original article by A.N. Shiryaev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article