Revision as of 07:54, 26 March 2012
Let 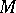 be a smooth manifold (cf. also Differentiable manifold) and let
be a smooth manifold (cf. also Differentiable manifold) and let 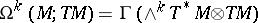 . One calls
. One calls
the space of all vector-valued differential forms. The Frölicher–Nijenhuis bracket 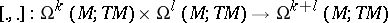 is a
is a 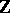 -graded Lie bracket:
-graded Lie bracket:
It extends the Lie bracket of smooth vector fields, since 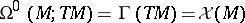 . The identity on
. The identity on 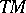 generates the one-dimensional centre. It is called the Frölicher–Nijenhuis bracket since it appeared with its full properties for the first time in [a1], after some indication in [a8]. One formula for it is:
generates the one-dimensional centre. It is called the Frölicher–Nijenhuis bracket since it appeared with its full properties for the first time in [a1], after some indication in [a8]. One formula for it is:
where 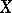 and
and 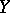 are vector fields,
are vector fields, 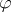 is a
is a 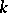 -form, and
-form, and 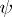 is an
is an 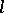 -form. It is a bilinear differential operator of bi-degree
-form. It is a bilinear differential operator of bi-degree 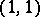 .
.
The Frölicher–Nijenhuis bracket is natural in the same way as the Lie bracket for vector fields: if  is smooth and
is smooth and 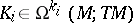 are
are 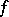 -related to
-related to 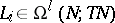 , then
, then 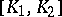 is also
is also 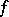 -related to
-related to 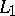 ,
,  .
.
Details.
A convenient source is [a3], Sect. 8. The basic formulas of the calculus of differential forms extend naturally to include the Frölicher–Nijenhuis bracket: Let
be the algebra of differential forms. One denotes by 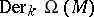 the space of all (graded) derivations of degree
the space of all (graded) derivations of degree 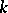 , i.e. all bounded linear mappings
, i.e. all bounded linear mappings 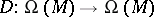 with
with 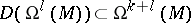 and
and 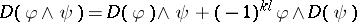 for
for  . The space
. The space 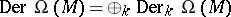 is a
is a 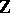 -graded Lie algebra with the graded commutator
-graded Lie algebra with the graded commutator 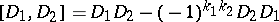 as bracket.
as bracket.
A derivation 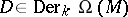 with
with 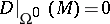 satisfies
satisfies 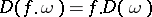 for
for 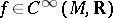 , thus
, thus 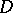 is of tensorial character and induces a derivation
is of tensorial character and induces a derivation 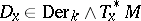 for each
for each 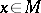 . It is uniquely determined by its restriction to
. It is uniquely determined by its restriction to  -forms
-forms 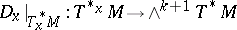 , which can be viewed as an element
, which can be viewed as an element 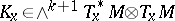 depending smoothly on
depending smoothly on 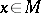 ; this is expressed by writing
; this is expressed by writing 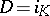 , where
, where  , and one has
, and one has
for  and
and  (or
(or  ).
).
By putting 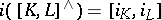 , one obtains a bracket
, one obtains a bracket 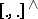 on
on 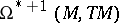 which defines a graded Lie algebra structure with the grading as indicated, and for
which defines a graded Lie algebra structure with the grading as indicated, and for 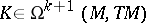 ,
, 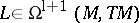 one has
one has
where 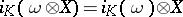 . The bracket
. The bracket  is called the the Nijenhuis–Richardson bracket, see [a6] and [a7]. If viewed on a vector space
is called the the Nijenhuis–Richardson bracket, see [a6] and [a7]. If viewed on a vector space 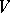 , it recognizes Lie algebra structures on
, it recognizes Lie algebra structures on 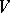 : A mapping
: A mapping 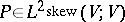 is a Lie bracket if and only if
is a Lie bracket if and only if 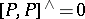 . This can be used to study deformations of Lie algebra structures:
. This can be used to study deformations of Lie algebra structures:  is again a Lie bracket on
is again a Lie bracket on 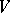 if and only if
if and only if 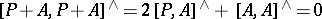 ; this can be written in the form of a Maurer–Cartan equation (cf. also Maurer–Cartan form) as
; this can be written in the form of a Maurer–Cartan equation (cf. also Maurer–Cartan form) as 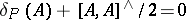 , since
, since 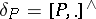 is the coboundary operator for the Chevalley cohomology (cf. also Cohomology) of the Lie algebra
is the coboundary operator for the Chevalley cohomology (cf. also Cohomology) of the Lie algebra 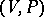 with values in the adjoint representation
with values in the adjoint representation 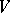 . See [a4] for a multi-graded elaboration of this.
. See [a4] for a multi-graded elaboration of this.
The exterior derivative 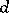 is an element of
is an element of 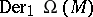 . In view of the formula
. In view of the formula 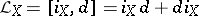 for vector fields
for vector fields 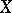 , one defines for
, one defines for 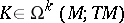 the Lie derivation
the Lie derivation 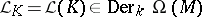 by
by 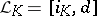 . The mapping
. The mapping 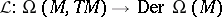 is injective. One has
is injective. One has  .
.
For any graded derivation 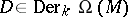 there are unique
there are unique 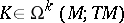 and
and 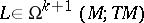 such that
such that
One has 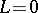 if and only if
if and only if 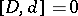 . Moreover,
. Moreover, 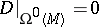 if and only if
if and only if 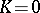 .
.
Let 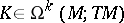 and
and 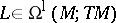 . Then, obviously,
. Then, obviously, 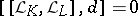 , so
, so
for a uniquely defined 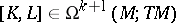 . This vector-valued form
. This vector-valued form 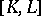 is the Frölicher–Nijenhuis bracket of
is the Frölicher–Nijenhuis bracket of 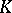 and
and 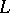 .
.
For 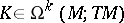 and
and 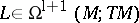 one has
one has
The space 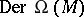 is a graded module over the graded algebra
is a graded module over the graded algebra 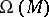 with the action
with the action 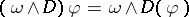 , because
, because 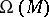 is graded commutative. Let the degree of
is graded commutative. Let the degree of 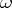 be
be 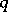 , of
, of  be
be 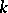 , and of
, and of 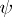 be
be 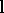 . Let the other degrees be as indicated. Then:
. Let the other degrees be as indicated. Then:
For 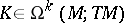 and
and 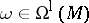 , the Lie derivative of
, the Lie derivative of 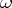 along
along 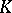 is given by:
is given by:
For  and
and 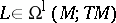 , the Frölicher–Nijenhuis bracket
, the Frölicher–Nijenhuis bracket 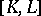 is given by:
is given by:
The Frölicher–Nijenhuis bracket expresses obstructions to integrability in many different situations: If 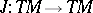 is an almost-complex structure, then
is an almost-complex structure, then 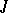 is complex structure if and only if the Nijenhuis tensor
is complex structure if and only if the Nijenhuis tensor 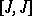 vanishes (the Newlander–Nirenberg theorem, [a5]). If
vanishes (the Newlander–Nirenberg theorem, [a5]). If 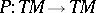 is a fibre-wise projection on the tangent spaces of a fibre bundle
is a fibre-wise projection on the tangent spaces of a fibre bundle 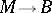 , then
, then 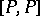 is a version of the curvature (see [a3], Sects. 9; 10). If
is a version of the curvature (see [a3], Sects. 9; 10). If 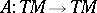 is fibre-wise diagonalizable with all eigenvalues real and of constant multiplicity, then the eigenspaces of
is fibre-wise diagonalizable with all eigenvalues real and of constant multiplicity, then the eigenspaces of 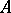 are integrable if and only if
are integrable if and only if 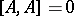 .
.
References
| [a1] | A. Frölicher, A. Nijenhuis, "Theory of vector valued differential forms. Part I." Indag. Math. , 18 (1956) pp. 338–359 |
| [a2] | A. Frölicher, A. Nijenhuis, "Invariance of vector form operations under mappings" Comment. Math. Helvetici , 34 (1960) pp. 227–248 |
| [a3] | I. Kolář, Peter W. Michor, J. Slovák, "Natural operations in differential geometry" , Springer (1993) |
| [a4] | Pierre Lecomte, Peter W. Michor, Hubert Schicketanz, "The multigraded Nijenhuis–Richardson Algebra, its universal property and application" J. Pure Appl. Algebra , 77 (1992) pp. 87–102 |
| [a5] | A. Newlander, L. Nirenberg, "Complex analytic coordinates in almost complex manifolds" Ann. of Math. , 65 (1957) pp. 391–404 |
| [a6] | A. Nijenhuis, R. Richardson, "Cohomology and deformations in graded Lie algebras" Bull. Amer. Math. Soc. , 72 (1966) pp. 1–29 |
| [a7] | A. Nijenhuis, R. Richardson, "Deformation of Lie algebra structures" J. Math. Mech. , 17 (1967) pp. 89–105 |
| [a8] | J.A. Schouten, "Über Differentialkonkomitanten zweier kontravarianten Grössen" Indag. Math. , 2 (1940) pp. 449–452 |
How to Cite This Entry:
Frölicher-Nijenhuis bracket. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%B6licher-Nijenhuis_bracket&oldid=23296
This article was adapted from an original article by Peter W. Michor (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article be a smooth manifold (cf. also Differentiable manifold) and let
be a smooth manifold (cf. also Differentiable manifold) and let 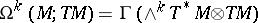 . One calls
. One calls
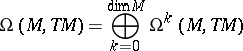
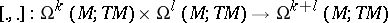 is a
is a 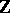 -graded Lie bracket:
-graded Lie bracket:
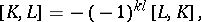
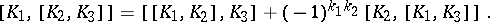
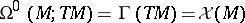 . The identity on
. The identity on 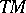 generates the one-dimensional centre. It is called the Frölicher–Nijenhuis bracket since it appeared with its full properties for the first time in [a1], after some indication in [a8]. One formula for it is:
generates the one-dimensional centre. It is called the Frölicher–Nijenhuis bracket since it appeared with its full properties for the first time in [a1], after some indication in [a8]. One formula for it is:
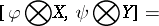
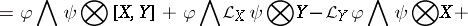
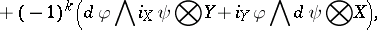
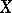 and
and 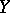 are vector fields,
are vector fields, 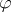 is a
is a 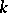 -form, and
-form, and 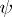 is an
is an 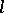 -form. It is a bilinear differential operator of bi-degree
-form. It is a bilinear differential operator of bi-degree 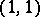 .
.
 is smooth and
is smooth and 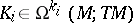 are
are 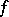 -related to
-related to 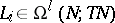 , then
, then 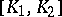 is also
is also 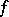 -related to
-related to 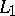 ,
,  .
.
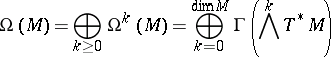
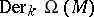 the space of all (graded) derivations of degree
the space of all (graded) derivations of degree 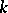 , i.e. all bounded linear mappings
, i.e. all bounded linear mappings 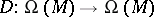 with
with 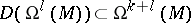 and
and 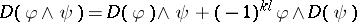 for
for  . The space
. The space 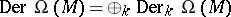 is a
is a 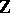 -graded Lie algebra with the graded commutator
-graded Lie algebra with the graded commutator 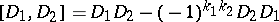 as bracket.
as bracket.
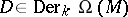 with
with 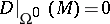 satisfies
satisfies 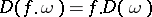 for
for 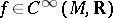 , thus
, thus 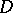 is of tensorial character and induces a derivation
is of tensorial character and induces a derivation 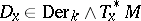 for each
for each 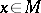 . It is uniquely determined by its restriction to
. It is uniquely determined by its restriction to 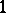 -forms
-forms 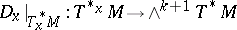 , which can be viewed as an element
, which can be viewed as an element 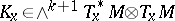 depending smoothly on
depending smoothly on 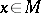 ; this is expressed by writing
; this is expressed by writing 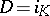 , where
, where  , and one has
, and one has

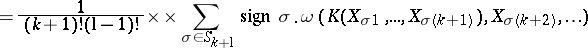
 and
and  (or
(or  ).
).
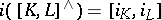 , one obtains a bracket
, one obtains a bracket 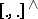 on
on 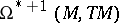 which defines a graded Lie algebra structure with the grading as indicated, and for
which defines a graded Lie algebra structure with the grading as indicated, and for 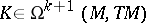 ,
, 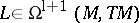 one has
one has
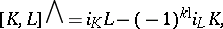
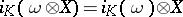 . The bracket
. The bracket  is called the the Nijenhuis–Richardson bracket, see [a6] and [a7]. If viewed on a vector space
is called the the Nijenhuis–Richardson bracket, see [a6] and [a7]. If viewed on a vector space 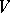 , it recognizes Lie algebra structures on
, it recognizes Lie algebra structures on 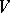 : A mapping
: A mapping 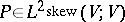 is a Lie bracket if and only if
is a Lie bracket if and only if 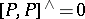 . This can be used to study deformations of Lie algebra structures:
. This can be used to study deformations of Lie algebra structures:  is again a Lie bracket on
is again a Lie bracket on 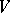 if and only if
if and only if 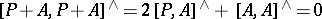 ; this can be written in the form of a Maurer–Cartan equation (cf. also Maurer–Cartan form) as
; this can be written in the form of a Maurer–Cartan equation (cf. also Maurer–Cartan form) as 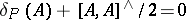 , since
, since 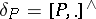 is the coboundary operator for the Chevalley cohomology (cf. also Cohomology) of the Lie algebra
is the coboundary operator for the Chevalley cohomology (cf. also Cohomology) of the Lie algebra 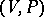 with values in the adjoint representation
with values in the adjoint representation 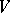 . See [a4] for a multi-graded elaboration of this.
. See [a4] for a multi-graded elaboration of this.
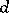 is an element of
is an element of 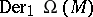 . In view of the formula
. In view of the formula 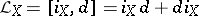 for vector fields
for vector fields 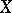 , one defines for
, one defines for 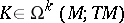 the Lie derivation
the Lie derivation 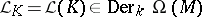 by
by 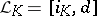 . The mapping
. The mapping 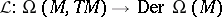 is injective. One has
is injective. One has  .
.
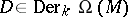 there are unique
there are unique 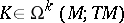 and
and 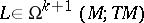 such that
such that
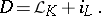
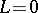 if and only if
if and only if 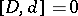 . Moreover,
. Moreover, 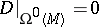 if and only if
if and only if 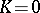 .
.
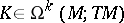 and
and 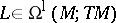 . Then, obviously,
. Then, obviously, 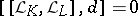 , so
, so

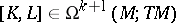 . This vector-valued form
. This vector-valued form 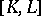 is the Frölicher–Nijenhuis bracket of
is the Frölicher–Nijenhuis bracket of 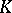 and
and 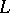 .
.
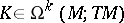 and
and 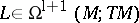 one has
one has
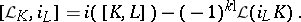
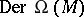 is a graded module over the graded algebra
is a graded module over the graded algebra 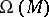 with the action
with the action 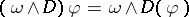 , because
, because 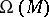 is graded commutative. Let the degree of
is graded commutative. Let the degree of 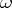 be
be 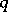 , of
, of  be
be 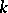 , and of
, and of 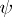 be
be  . Let the other degrees be as indicated. Then:
. Let the other degrees be as indicated. Then:
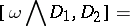
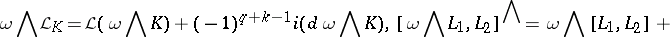
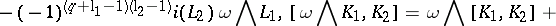
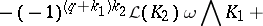
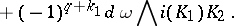
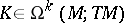 and
and 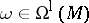 , the Lie derivative of
, the Lie derivative of 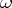 along
along 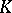 is given by:
is given by:
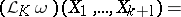
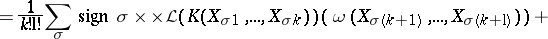
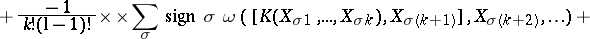
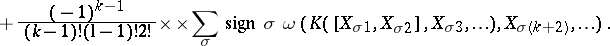
 and
and 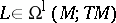 , the Frölicher–Nijenhuis bracket
, the Frölicher–Nijenhuis bracket 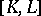 is given by:
is given by:
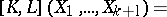
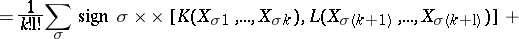
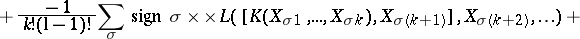
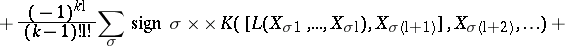
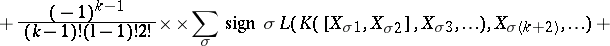
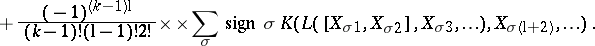
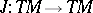 is an almost-complex structure, then
is an almost-complex structure, then 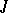 is complex structure if and only if the Nijenhuis tensor
is complex structure if and only if the Nijenhuis tensor 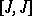 vanishes (the Newlander–Nirenberg theorem, [a5]). If
vanishes (the Newlander–Nirenberg theorem, [a5]). If 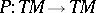 is a fibre-wise projection on the tangent spaces of a fibre bundle
is a fibre-wise projection on the tangent spaces of a fibre bundle 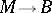 , then
, then 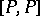 is a version of the curvature (see [a3], Sects. 9; 10). If
is a version of the curvature (see [a3], Sects. 9; 10). If 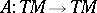 is fibre-wise diagonalizable with all eigenvalues real and of constant multiplicity, then the eigenspaces of
is fibre-wise diagonalizable with all eigenvalues real and of constant multiplicity, then the eigenspaces of 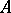 are integrable if and only if
are integrable if and only if 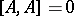 .
.