Difference between revisions of "De la Vallée-Poussin summation method"
Ulf Rehmann (talk | contribs) m (moved De la Vallée-Poussin summation method to De la Vallee-Poussin summation method: ascii title) |
Ulf Rehmann (talk | contribs) m (moved De la Vallee-Poussin summation method to De la Vallée-Poussin summation method over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
A method for summing series of numbers. It is denoted by the symbol 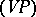 . A series
. A series
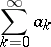 |
has a de la Vallée-Poussin sum 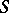 if the relation
if the relation
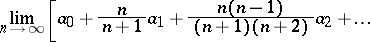 |
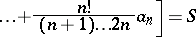 |
is valid. The method was proposed by Ch.J. de la Vallée-Poussin [1]. For the Fourier series of a function 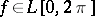 the de la Vallée-Poussin averages (see also de la Vallée-Poussin singular integral) are of the form
the de la Vallée-Poussin averages (see also de la Vallée-Poussin singular integral) are of the form
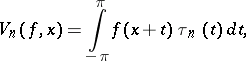 |
where
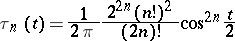 |
is the so-called de la Vallée-Poussin kernel. The de la Vallée-Poussin summation method is a regular summation method (cf. Regular summation methods). The method is stronger than all Cesàro summation methods (cf. Inclusion of summation methods). In view of its weak approximative properties, the de la Vallée-Poussin summation method is practically never used in the theory of approximation of functions.
References
| [1] | Ch.J. de la Vallée-Poussin, "Sur l'approximation des fonctions d'une variable reélle et de leurs dérivées par des polynômes et des suites limitées de Fourier" Bull. Acad. Belg. , 3 (1908) pp. 193–254 |
| [2] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [3] | T. Gronwall, "Ueber einige Summationsmethoden und ihre Anwendung auf die Fouriersche Reihe" J. Reine Angew. Math. , 147 (1917) pp. 16–35 |
De la Vallée-Poussin summation method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_summation_method&oldid=23252