Difference between revisions of "De la Vallée-Poussin sum"
Ulf Rehmann (talk | contribs) m (moved De la Vallée-Poussin sum to De la Vallee-Poussin sum: ascii title) |
Ulf Rehmann (talk | contribs) m (moved De la Vallee-Poussin sum to De la Vallée-Poussin sum over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
The expression
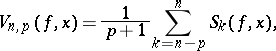 | (*) |
 |
where 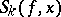 ,
, 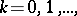 are the partial sums of the Fourier series of a function
are the partial sums of the Fourier series of a function 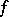 with period
with period 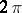 . If
. If 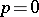 , the de la Vallée-Poussin sums become identical with the partial Fourier sums, and if
, the de la Vallée-Poussin sums become identical with the partial Fourier sums, and if  , they become identical with the Fejér sums (cf. Fejér sum). Ch.J. de la Vallée-Poussin [1], [2] was the first to study the method of approximating periodic functions by polynomials of the form (*); he also established the inequality
, they become identical with the Fejér sums (cf. Fejér sum). Ch.J. de la Vallée-Poussin [1], [2] was the first to study the method of approximating periodic functions by polynomials of the form (*); he also established the inequality
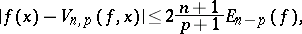 |
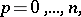 |
where 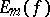 is the best uniform approximation of the function
is the best uniform approximation of the function 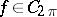 using trigonometric polynomials of order not greater than
using trigonometric polynomials of order not greater than 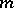 . If
. If 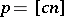 ,
, 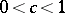 and
and 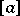 is the integer part of the number
is the integer part of the number  , the polynomials
, the polynomials 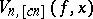 realize an approximation of order
realize an approximation of order 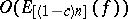 . The polynomials
. The polynomials 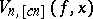 yield the best order approximations of continuous functions of period
yield the best order approximations of continuous functions of period 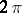 , with an estimate
, with an estimate 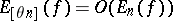 for certain values of
for certain values of 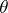 ,
, 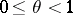 . The de la Vallée-Poussin sums have several properties which are of interest in the theory of summation of Fourier series. For instance, if
. The de la Vallée-Poussin sums have several properties which are of interest in the theory of summation of Fourier series. For instance, if 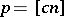 ,
, 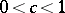 , then
, then 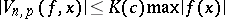 , and if
, and if 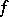 is a trigonometric polynomial of order not exceeding
is a trigonometric polynomial of order not exceeding 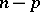 , then
, then 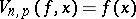 . A de la Vallée-Poussin sum may be written as follows
. A de la Vallée-Poussin sum may be written as follows
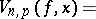 |
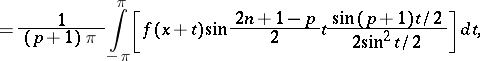 |
where the expressions
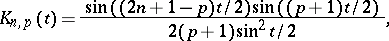 |
 |
are said to be the de la Vallée-Poussin kernels.
References
| [1] | Ch.J. de la Vallée-Poussin, "Sur la meilleure approximation des fonctions d'une variable réelle par des expressions d'ordre donné" C.R. Acad. Sci. Paris Sér. I. Math. , 166 (1918) pp. 799–802 |
| [2] | Ch.J. de la Vallée-Poussin, "Leçons sur l'approximation des fonctions d'une variable réelle" , Gauthier-Villars (1919) |
| [3] | I.P. Natanson, "Constructive function theory" , 1 , F. Ungar (1964) (Translated from Russian) |
| [4] | P.P. Korovkin, "Linear operators and approximation theory" , Hindushtan Publ. Comp. (1960) (Translated from Russian) |
| [5] | S.M. Nikol'skii, "Sur certaines méthodes d'approximation au moyen de sommes trigonométriques" Izv. Akad. Nauk SSSR Ser. Mat. , 4 : 6 (1940) pp. 509–520 |
| [6] | S.B. Stechkin, "On de la Vallée-Poussin sums" Dokl. Akad. Nauk SSSR , 80 : 4 (1951) pp. 545–520 (In Russian) |
| [7] | A.D. Shcherbina, "On a summation method of series, conjugate to Fourier series" Mat. Sb. , 27 (69) : 2 (1950) pp. 157–170 (In Russian) |
| [8] | A.F. Timan, "Approximation properties of linear methods of summation of Fourier series" Izv. Akad. Nauk SSSR Ser. Mat. , 17 (1953) pp. 99–134 (In Russian) |
| [9] | A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) (Translated from Russian) |
| [10] | A.V. Efimov, "On approximation of periodic functions by de la Vallée-Poussin sums" Izv. Akad. Nauk SSSR Ser. Mat. , 23 : 5 (1959) pp. 737–770 (In Russian) |
| [11] | A.V. Efimov, "On approximation of periodic functions by de la Vallée-Poussin sums" Izv. Akad. Nauk SSSR Ser. Mat. , 24 : 3 (1960) pp. 431–468 (In Russian) |
| [12] | S.A. Telyakovskii, "Approximation of differentiable functions by de la Vallée-Poussin sums" Dokl. Akad. Nauk SSSR , 121 : 3 (1958) pp. 426–429 (In Russian) |
| [13] | S.A. Telyakovskii, "Approximation to functions differentiable in Weyl's sense by de la Vallée-Poussin sums" Soviet Math. Dokl. , 1 : 2 (1960) pp. 240–243 Dokl. Akad. Nauk SSSR , 131 : 2 (1960) pp. 259–262 |
Comments
The de la Vallée-Poussin kernels are also given by the following formula, which in a way most clearly reveals their structure:
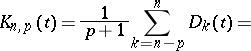 |
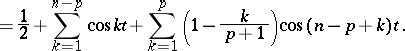 |
Here the 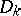 (
(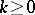 ) are the Dirichlet kernels (cf. Dirichlet kernel).
) are the Dirichlet kernels (cf. Dirichlet kernel).
De la Vallée-Poussin sum. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=De_la_Vall%C3%A9e-Poussin_sum&oldid=23250