Difference between revisions of "Carathéodory class"
Ulf Rehmann (talk | contribs) m (moved Carathéodory class to Caratheodory class: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Caratheodory class to Carathéodory class over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
The class 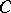 of functions
of functions
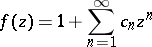 |
that are regular in the disc 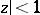 and have positive real part there. The class is named after C. Carathéodory, who determined the precise set of values of the system of coefficients
and have positive real part there. The class is named after C. Carathéodory, who determined the precise set of values of the system of coefficients 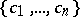 ,
, 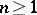 , on the class
, on the class 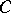 (see [1], [2]).
(see [1], [2]).
The Riesz–Herglotz theorem. In order that 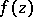 be of class
be of class 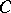 it is necessary and sufficient that it have a Stieltjes integral representation
it is necessary and sufficient that it have a Stieltjes integral representation
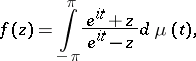 |
where 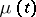 is a non-decreasing function on
is a non-decreasing function on 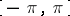 such that
such that 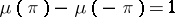 .
.
By means of this representation it is easy to deduce integral parametric representations for classes of functions which are convex and univalent in the disc, star-shaped and univalent in the disc, and others.
The Carathéodory–Toeplitz theorem. The set of values of the system 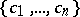 ,
, 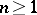 , on
, on 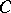 is the closed convex bounded set
is the closed convex bounded set 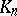 of points of the
of points of the  -dimensional complex Euclidean space at which the determinants
-dimensional complex Euclidean space at which the determinants
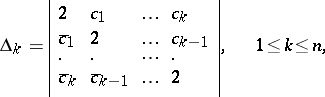 |
are either all positive, or positive up to some number, beyond which they are all zero. In the latter case one obtains a face 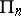 of the coefficient body
of the coefficient body 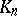 . Corresponding to each point of
. Corresponding to each point of 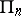 there is just one function in the class
there is just one function in the class 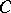 , which has the form
, which has the form
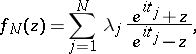 |
where
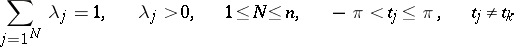 |
for 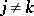 ,
, 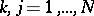 .
.
The set of values of the coefficients 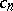 ,
, 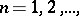 on
on 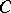 is the disc
is the disc 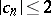 ; the only functions corresponding to the circle
; the only functions corresponding to the circle 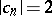 are
are
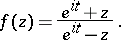 |
The set of values of 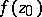 (
(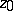 fixed,
fixed, 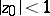 ) on
) on 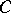 is the disc whose diameter is the interval
is the disc whose diameter is the interval 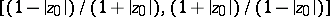 ; the only functions corresponding to the boundary of this disc are
; the only functions corresponding to the boundary of this disc are
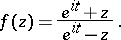 |
Sets of values of systems of functionals of a more general type have also been considered (see [6]). For the class 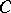 , variational formulas have been obtained by means of which a number of extremal problems in the class
, variational formulas have been obtained by means of which a number of extremal problems in the class 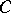 are solved by the functions
are solved by the functions 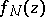 ,
, 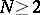 (see [6]).
(see [6]).
The main subclass of 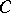 is the class
is the class 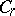 of functions
of functions 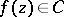 having real coefficients
having real coefficients 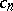 ,
, 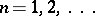 . In order that
. In order that 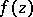 belong to the class
belong to the class 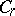 it is necessary and sufficient that it have a representation
it is necessary and sufficient that it have a representation
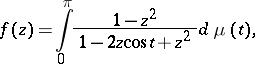 |
where 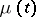 is a non-decreasing function on
is a non-decreasing function on 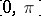 such that
such that 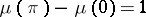 . By means of this representation many extremal problems in the class
. By means of this representation many extremal problems in the class 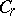 are solved.
are solved.
References
| [1] | C. Carathéordory, "Über den Variabilitätsbereich der Koeffizienten von Potenzreihen, die gegebene Werte nicht annehmen" Math. Ann. , 64 (1907) pp. 95–115 |
| [2] | C. Carathéodory, "Über den Variabilitätsbereich der Fourier'schen Konstanten von positiven harmonischen Funktionen" Rend. Circ. Mat. Palermo , 32 (1911) pp. 193–217 |
| [3] | O. Toeplitz, "Ueber die Fourier'sche Entwicklung positiver Funktionen" Rend. Circ. Mat. Palermo , 32 (1911) pp. 191–192 |
| [4] | F. Riesz, "Sur certains systèmes singuliers d'equations intégrales" Ann. Sci. Ecole Norm. Super. , 28 (1911) pp. 33–62 |
| [5] | G. Herglotz, "Über Potenzreihen mit positiven, reellen Teil im Einheitskreis" Ber. Verhandl. Sächs. Akad. Wiss. Leipzig. Math.-Nat. Kl. , 63 (1911) pp. 501–511 |
| [6] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
Carathéodory class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carath%C3%A9odory_class&oldid=23212