Difference between revisions of "Arzelà variation"
Ulf Rehmann (talk | contribs) m (moved Arzelà variation to Arzela variation: ascii title) |
Ulf Rehmann (talk | contribs) m (moved Arzela variation to Arzelà variation over redirect: accented title) |
(No difference)
| |
Revision as of 07:54, 26 March 2012
A numerical characteristic of a function of several variables, which may be regarded as the multi-dimensional analogue of the variation of a function in one unknown. Let 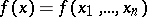 be a real-valued function given on an
be a real-valued function given on an  -dimensional parallelepipedon
-dimensional parallelepipedon 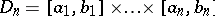 ,
, 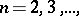 and let
and let 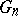 be the class of all continuous vector functions
be the class of all continuous vector functions 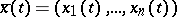 ,
, 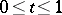 , such that each of the functions
, such that each of the functions 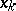 is non-decreasing on
is non-decreasing on 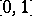 , and with
, and with 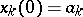 ,
, 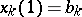 ,
, 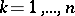 . Then
. Then
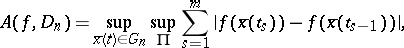 |
where 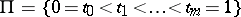 is an arbitrary system of points in
is an arbitrary system of points in 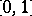 . This definition for the case
. This definition for the case 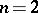 was proposed by C. Arzelà [1] (see also [2], p. 543). If
was proposed by C. Arzelà [1] (see also [2], p. 543). If  , one says that
, one says that 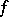 has bounded (finite) Arzelà variation on
has bounded (finite) Arzelà variation on 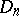 , and the class of all such functions is denoted by
, and the class of all such functions is denoted by 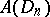 . For a function
. For a function  to belong to the class
to belong to the class  it is necessary and sufficient that there exists a decomposition
it is necessary and sufficient that there exists a decomposition 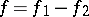 , where
, where 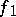 and
and 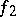 are finite non-decreasing functions on
are finite non-decreasing functions on  . A function
. A function 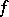 is called non-decreasing on
is called non-decreasing on 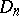 if
if
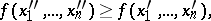 |
for 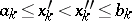 (
(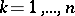 ). The class
). The class  contains the class of functions of bounded Hardy variation on
contains the class of functions of bounded Hardy variation on 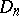 .
.
References
| [1] | C. Arzelà, Rend. Accad. Sci. Bologna , 9 : 2 (1905) pp. 100–107 |
| [2] | H. Hahn, "Theorie der reellen Funktionen" , 1 , Springer (1921) |
Arzelà variation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arzel%C3%A0_variation&oldid=23184