Saxon-Hutner theorem

A theorem concerning energy gaps in one-dimensional random alloy models described by the Schrödinger equation or the Dirac equation. It states that forbidden energies that are common to a pure crystal and a pure crystal 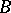(with the same lattice constant) will always be forbidden energies in any arrangement of the atoms of 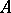and 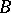in a substitutional solid solution.

Making use of the one-to-one correspondence between the real localized atomic potentials and 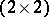-transfer matrices belonging to any of the isomorphic three-dimensional Lie groups 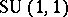, 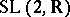or 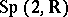, this can be described in mathematical terms as follows. If 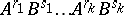is an arbitrary linear chain consisting of two types of atoms 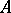and 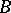, each having representatives 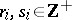in the 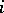th period. Then the group nature of the individual transfer matrices 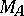and 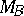makes it possible to express the total transfer matrix 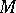of the elementary cell as the product , and the forbidden energies for electrons propagating there are given by the condition .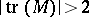

In the transfer-matrix approach, the theorem takes the form of the following question: Given that

is it true that for any arrangement 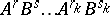of atoms of type 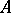and 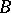one has

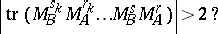Relying on quite different techniques, several non-equivalent sufficient conditions guaranteeing its validity have been derived.

References

[a1]	D. Saxon, R. Hutner, Philips Res. Rep. , 4 (1949) pp. 81
[a2]	H. Matsuda, Progr. Theor. Phys. , 27 (1962) pp. 81
[a3]	J. Hori, Progr. Theor. Phys. , 32 (1964) pp. 371
[a4]	L. Dworin, Phys. Rev. , 138 A (1965) pp. 1121
[a5]	B. Tong, S. Tong, Phys. Rev. , 180 (1969) pp. 739
[a6]	I. Mladenov, C.R. Acad. Sci. (Sofia) , 38 (1985) pp. 993
[a7]	I. Mladenov, Phys. Lett. A , 137 (1989) pp. 313