Difference between revisions of "Putnam-Fuglede theorems"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Putnam–Fuglede theorems to Putnam-Fuglede theorems: ascii title) |
(No difference)
| |
Revision as of 18:54, 24 March 2012
Fuglede–Putnam theorems, Berberian–Putnam–Fuglede theorems
Let 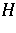 denote a Hilbert space,
denote a Hilbert space, 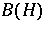 the algebra of operators on
the algebra of operators on 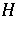 (i.e., bounded linear transformations; cf. Linear transformation; Operator),
(i.e., bounded linear transformations; cf. Linear transformation; Operator), 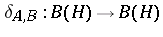 the derivation
the derivation 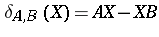 (
(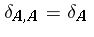 ; cf. also Derivation in a ring) and let
; cf. also Derivation in a ring) and let 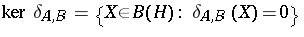 . If
. If 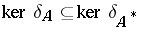 , then
, then 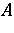 is normal (cf. Normal operator; simply choose
is normal (cf. Normal operator; simply choose 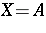 in
in 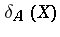 ). The question whether the converse assertion, namely "Is kerdAkerdA* for normal A?" , also holds was raised by J. von Neumann in 1942, and answered in the affirmative in 1950 by B. Fuglede [a7], p. 349,
). The question whether the converse assertion, namely "Is kerdAkerdA* for normal A?" , also holds was raised by J. von Neumann in 1942, and answered in the affirmative in 1950 by B. Fuglede [a7], p. 349,  45. C.R. Putnam extended the Fuglede theorem to
45. C.R. Putnam extended the Fuglede theorem to 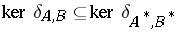 , for normal
, for normal 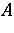 and
and 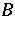 [a7], p. 352,
[a7], p. 352,  109, and a beautiful proof of the Putnam–Fuglede theorem was given by M. Rosenblum [a7], p. 352,
109, and a beautiful proof of the Putnam–Fuglede theorem was given by M. Rosenblum [a7], p. 352,  118. Introducing the trick of considering the operators
118. Introducing the trick of considering the operators 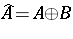 and
and 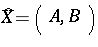 on
on  , S.K. Berberian [a7], p. 347,
, S.K. Berberian [a7], p. 347, 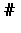 9, showed that the Putnam–Fuglede theorem indeed follows from the Fuglede theorem. For this reason, Putnam–Fuglede theorems are sometimes also referred to as Berberian–Putnam–Fuglede theorems.
9, showed that the Putnam–Fuglede theorem indeed follows from the Fuglede theorem. For this reason, Putnam–Fuglede theorems are sometimes also referred to as Berberian–Putnam–Fuglede theorems.
The Putnam–Fuglede theorem, namely "kerdA,BkerdA*,B* for normal A and B" , has since been considered in a large number of papers, and various generalizations of it have appeared over the past four decades. Broadly speaking, these generalizations fall into the following four types:
i) where the normality is replaced by a weaker requirement, such as subnormality or 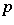 -hyponormality;
-hyponormality;
ii) asymptotic Putnam–Fuglede theorems;
iii) Putnam–Fuglede theorems modulo (proper, two-sided) ideals of 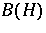 ; and
; and
iv) Putnam–Fuglede theorems in a 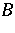 -space setting. Before briefly examining some of these, note that there exist subnormal operators
-space setting. Before briefly examining some of these, note that there exist subnormal operators 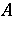 and
and 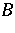 for which
for which 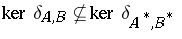 [a7], p. 107. This implies that in any generalization of the Putnam–Fuglede theorem to a wider class of operators, the hypotheses on
[a7], p. 107. This implies that in any generalization of the Putnam–Fuglede theorem to a wider class of operators, the hypotheses on 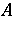 and
and 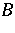 are not symmetric (and that it is more appropriate to think of
are not symmetric (and that it is more appropriate to think of 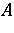 and
and 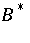 as being normal in the Putnam–Fuglede theorem).
as being normal in the Putnam–Fuglede theorem).
Asymmetric Putnam–Fuglede theorems.
If 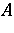 and
and  are subnormal operators with normal extensions
are subnormal operators with normal extensions 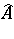 and
and 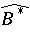 on
on 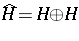 (say) and
(say) and 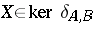 , then
, then 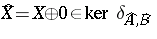 , and it follows that
, and it follows that 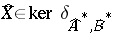 and
and 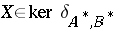 . This asymmetric extension of the Putnam–Fuglede theorem was proved by T. Furuta [a6] (though an avatar of this result had already appeared in [a10]). Following a lot of activity during the 1970s and the 1980s ([a2], [a5], [a6], [a9] list some of the references), it is now (1998) known that
. This asymmetric extension of the Putnam–Fuglede theorem was proved by T. Furuta [a6] (though an avatar of this result had already appeared in [a10]). Following a lot of activity during the 1970s and the 1980s ([a2], [a5], [a6], [a9] list some of the references), it is now (1998) known that 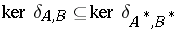 for
for 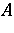 and
and 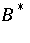 belonging to a large number of suitably paired classes of operators, amongst them
belonging to a large number of suitably paired classes of operators, amongst them  -hyponormal (
-hyponormal (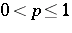 ),
), 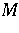 -hyponormal, dominant and
-hyponormal, dominant and 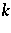 -quasi-hyponormal classes [a5].
-quasi-hyponormal classes [a5].
Asymptotic Putnam–Fuglede theorems.
Given normal 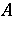 and
and 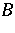 , and a neighbourhood
, and a neighbourhood  of
of 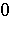 in some topology (weak operator, strong operator or uniform), does there exist a neighbourhood
in some topology (weak operator, strong operator or uniform), does there exist a neighbourhood 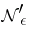 of
of 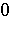 in the same topology such that
in the same topology such that 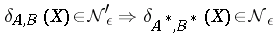 ? The answer to this question is (in general) no, for there exists a normal
? The answer to this question is (in general) no, for there exists a normal  and a (non-uniformly bounded) sequence
and a (non-uniformly bounded) sequence 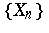 of operators such that
of operators such that 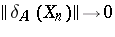 but
but 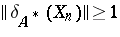 for all
for all 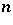 [a8]. If, however, the sequence
[a8]. If, however, the sequence  is uniformly bounded, then the answer is in the affirmative for normal (and subnormal)
is uniformly bounded, then the answer is in the affirmative for normal (and subnormal) 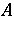 and
and 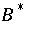 [a2] (and indeed, if one limits oneself to the uniform topology, for a number of classes of operators [a5], [a9]).
[a2] (and indeed, if one limits oneself to the uniform topology, for a number of classes of operators [a5], [a9]).
Putnam–Fuglede theorems modulo ideals.
Say that the Putnam–Fuglede theorem holds modulo an ideal 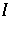 if, given normal operators
if, given normal operators 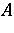 and
and 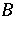 ,
, 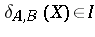 implies
implies 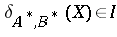 for all
for all  . The Putnam–Fuglede theorem holds modulo the compacts (simply consider the Putnam–Fuglede theorem in the Calkin algebra), and does not hold modulo the ideal of finite-rank operators. In a remarkable extension of the Putnam–Fuglede theorem to Schatten-von Neumann ideals
. The Putnam–Fuglede theorem holds modulo the compacts (simply consider the Putnam–Fuglede theorem in the Calkin algebra), and does not hold modulo the ideal of finite-rank operators. In a remarkable extension of the Putnam–Fuglede theorem to Schatten-von Neumann ideals 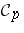 ,
, 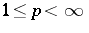 (cf. also Calderón couples), G. Weiss proved in [a12] that
(cf. also Calderón couples), G. Weiss proved in [a12] that 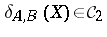 implies
implies 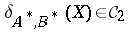 . It has since been proved that the Putnam–Fuglede theorem holds modulo
. It has since been proved that the Putnam–Fuglede theorem holds modulo 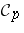 for all
for all 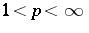 [a1], [a12], and also with normal
[a1], [a12], and also with normal 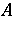 ,
, 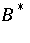 replaced by subnormal
replaced by subnormal  ,
, 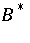 . It is not known if the Putnam–Fuglede theorem holds modulo
. It is not known if the Putnam–Fuglede theorem holds modulo 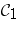 .
.
Banach space formulation of the Putnam–Fuglede theorem.
Letting 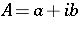 and
and 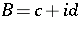 , where
, where 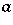 ,
, 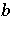 ,
, 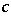 ,
, 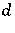 are self-adjoint operators such that
are self-adjoint operators such that 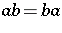 and
and 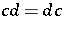 (cf. also Self-adjoint operator), the Putnam–Fuglede theorem can be written as
(cf. also Self-adjoint operator), the Putnam–Fuglede theorem can be written as
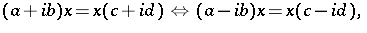 |
or, equivalently,
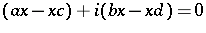 |
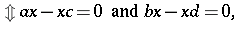 |
for all 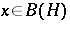 . Defining
. Defining 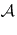 and
and 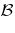 by
by  and
and 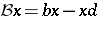 , it is seen that
, it is seen that 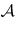 and
and 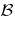 are Hermitian (i. e., the one-parameter groups
are Hermitian (i. e., the one-parameter groups 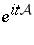 and
and 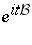 ,
, 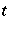 a real number, are groups of isometries on the Banach space
a real number, are groups of isometries on the Banach space 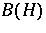 ) which commute. The Putnam–Fuglede theorem now says that if
) which commute. The Putnam–Fuglede theorem now says that if 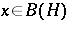 and
and  , then
, then  . This version of the Putnam–Fuglede theorem has been generalized to the Banach space setting as follows: if
. This version of the Putnam–Fuglede theorem has been generalized to the Banach space setting as follows: if 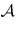 and
and 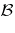 are commuting Hermitian operators on a complex Banach space
are commuting Hermitian operators on a complex Banach space 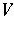 , then, given
, then, given  ,
,
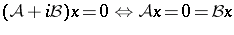 |
(see [a3], [a4] for more general results).
References
| [a1] | A. Abdessemed, E.B. Davies, "Some commutator estimates in the Schatten classes" J. London Math. Soc. , 39 (1989) pp. 299–308 |
| [a2] | S.T.M. Ackermans, S.J.L. Eijndhoven, F.J.L. Martens, "On almost commuting operators" Nederl. Akad. Wetensch. Proc. Ser. A , 86 (1983) pp. 389–391 |
| [a3] | K. Boydazhiev, "Commuting  groups and the Fuglede–Putnam theorem" Studia Math. , 81 (1985) pp. 303–306 groups and the Fuglede–Putnam theorem" Studia Math. , 81 (1985) pp. 303–306 |
| [a4] | M.J. Crabb, P.G. Spain, "Commutators and normal operators" Glasgow Math. J. , 18 (1977) pp. 197–198 |
| [a5] | B.P. Duggal, "On generalised Putnam–Fuglede theorems" Monatsh. Math. , 107 (1989) pp. 309–332 (See also: On quasi-similar hyponormal operators, Integral Eq. Oper. Th. 26 (1996), 338-345) |
| [a6] | T. Furuta, "On relaxation of normality in the Fuglede–Putnam theorem" Proc. Amer. Math. Soc. , 77 (1979) pp. 324–328 |
| [a7] | P.R. Halmos, "A Hilbert space problem book" , Springer (1982) |
| [a8] | B.E. Johnson, J.P. Williams, "The range of a normal derivation" Pacific J. Math. , 58 (1975) pp. 105–122 |
| [a9] | M. Radjabalipour, "An extension of Putnam–Fuglede theorem for hyponormal operators" Math. Z. , 194 (1987) pp. 117–120 |
| [a10] | H. Radjavi, P. Rosenthal, "On roots of normal operators" J. Math. Anal. Appl. , 34 (1971) pp. 653–664 |
| [a11] | V. Shulman, "Some remarks on the Fuglede–Weiss Theorem" Bull. London Math. Soc. , 28 (1996) pp. 385–392 |
| [a12] | G. Weiss, "The Fuglede commutativity theorem modulo the Hilbert–Schmidt class and generating functions I" Trans. Amer. Math. Soc. , 246 (1978) pp. 193–209 (See also: II, J. Operator Th. 5 (1981), 3-16) |
Putnam-Fuglede theorems. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Putnam-Fuglede_theorems&oldid=22959