Perron-Frobenius theorem

Let a real square 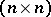-matrix 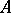be considered as an operator on 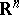, let it be without invariant coordinate subspaces (such a matrix is called indecomposable) and let it be non-negative (i.e. all its elements are non-negative). Also, let be its eigen values, enumerated such that

Then,

1) the number is a simple positive root of the characteristic polynomial of ;

2) there exists an eigen vector of 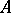with positive coordinates corresponding to ;

3) the numbers coincide, apart from their numbering, with the numbers , where ;

4) the product of any eigen value of 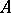by 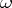is an eigen value of ;

5) for 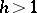one can find a permutation of the rows and columns that reduces to the form

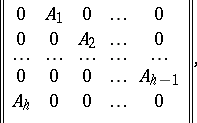where 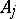is a matrix of order .

O. Perron proved the assertions 1) and 2) for positive matrices in [1], while G. Frobenius [2] gave the full form of the theorem.

References

[1]	O. Perron, "Zur Theorie der Matrizen" Math. Ann. , 64 (1907) pp. 248–263
[2]	G. Frobenius, "Ueber Matrizen aus nicht negativen Elementen" Sitzungsber. Königl. Preuss. Akad. Wiss. (1912) pp. 456–477
[3]	F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian)

Comments

The Perron–Frobenius theorem has numerous applications, cf. [a1], [a2].

References

[a1]	E. Seneta, "Nonnegative matrices" , Allen & Unwin (1973)
[a2]	K. Lancaster, "Mathematical economics" , Macmillan (1968)