Difference between revisions of "Michaelis-Menten equation"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Michaelis–Menten equation to Michaelis-Menten equation: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
The usual equation to describe the conversion of a substrate in an enzymatic reaction. Let 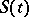 be the concentration of some substrate which is converted by an enzyme
be the concentration of some substrate which is converted by an enzyme 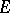 into a product
into a product 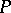 . The reaction rate is proportional to
. The reaction rate is proportional to  for small values of
for small values of 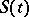 , but there is a maximum rate, which is not surpassed even for large
, but there is a maximum rate, which is not surpassed even for large 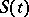 . These observations can be expressed by the equation
. These observations can be expressed by the equation
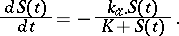 |
In this case the first reaction parameter, 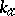 , describes the maximal conversion speed, and the second reaction parameter,
, describes the maximal conversion speed, and the second reaction parameter, 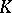 , is equal to the substrate concentration at which the reaction speed is exactly
, is equal to the substrate concentration at which the reaction speed is exactly  . For small values of
. For small values of 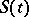 , the reaction rate is
, the reaction rate is 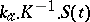 .
.
The equation can be derived from the chemical equilibrium reactions between the substrate 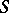 and the enzyme
and the enzyme 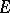 , which combine to a compound
, which combine to a compound 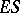 . This compound is rearranged in an equilibrium reaction into a compound
. This compound is rearranged in an equilibrium reaction into a compound 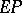 , which dissociates into the enzyme
, which dissociates into the enzyme 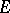 and product
and product 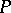 . In a formula:
. In a formula:
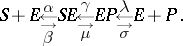 |
In this reaction, the step from 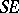 to
to 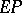 is usually far slower than the other reactions, and if the reaction from
is usually far slower than the other reactions, and if the reaction from 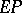 to
to 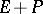 is irreversible, or if the product
is irreversible, or if the product 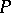 is removed by some transport mechanism, then the two reaction constants
is removed by some transport mechanism, then the two reaction constants 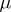 and
and  can be discarded, and the rearrangement coefficient
can be discarded, and the rearrangement coefficient 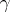 determines a simplified reaction equation:
determines a simplified reaction equation:
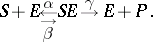 |
Putting 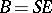 , the following system of differential equations emerges from the reactions:
, the following system of differential equations emerges from the reactions:
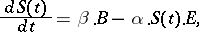 |
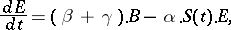 |
 |
These equations imply that 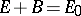 is a constant, representing the maximal amount of either
is a constant, representing the maximal amount of either 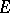 or
or 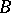 . Usually,
. Usually, 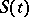 is large with respect to fluctuations in
is large with respect to fluctuations in 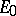 and so the reaction enters a steady state, in which the concentrations of
and so the reaction enters a steady state, in which the concentrations of 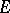 and
and  remain almost constant over a large time interval. In that case the proportion
remain almost constant over a large time interval. In that case the proportion 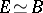 equals
equals 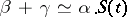 , which yields
, which yields
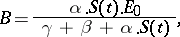 |
and
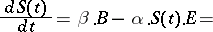 |
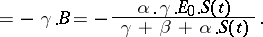 |
The values of 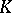 and
and  can be inferred from the differential equation. This gives:
can be inferred from the differential equation. This gives:
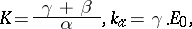 |
and so
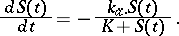 |
The values can be fitted from observations of 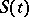 , but it is impossible to also find the parameters
, but it is impossible to also find the parameters 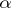 ,
, 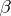 ,
, 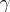 , and
, and 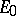 from the curve of
from the curve of 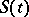 .
.
The equation was derived by L. Michaelis and M.L. Menten [a1].
References
| [a1] | L. Michaelis, M.L. Menten, "Die Kinetik der Invertinwirkung" Biochem. Zeitschrift , 2 (1913) pp. 333–369 |
Michaelis-Menten equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Michaelis-Menten_equation&oldid=22809