Mazur-Orlicz theorem

A sequence is said to be summable to by a method given by an infinite matrix , if

Let be the set of all sequences summables by a method . Such a method is said to be convergence preserving if contains all convergent sequences (it is not assumed, however, that for a convergent sequence one has ; if the latter holds, is called a permanent summability method). For a convergence-preserving method 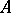there is a well-defined quantity

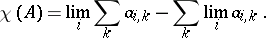Let 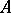and be convergence-preserving methods with , and assume that for each convergent sequence one has . Then the Mazur–Orlicz theorem is usually given to the following statement: If every bounded sequence in is in 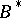, then also for these sequences ([a3], Thm. 2; see also [a1] and [a2]).

A related result is as follows. If 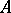is a convergence-preserving method, then 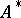contains an unbounded sequence if either of the following is satisfied ([a3], Thm. 7):

i) ;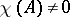

ii) and 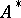contains a bounded divergent sequence. A permanent method is said to be perfectly inconsistent if for each divergent sequence in there is a permanent method 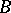with and .

A permanent method is perfectly inconsistent if and only if every sequence in is either convergent or unbounded ([a3], Thm. 10).

S. Mazur and W. Orlicz also worked also in functional analysis; e.g., the Banach–Steinhaus theorem for 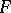-spaces (see Fréchet topology) is due to them.

References

[a1]	A.L. Brudno, "Summability of bounded sequences by means of matrices" Mat. Sb. , 16 (1949) pp. 191–247 (In Russian)
[a2]	S. Mazur, W. Orlicz, "Sur les mèthodes linèaires de sommation" C.R. Acad. Sci. Paris , 196 (1933) pp. 32–34
[a3]	S. Mazur, W. Orlicz, "On linear methods of summability" Studia Math. , 14 (1954) pp. 129–160