Difference between revisions of "Lindeberg-Feller theorem"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Lindeberg–Feller theorem to Lindeberg-Feller theorem: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
A theorem that establishes necessary and sufficient conditions for the asymptotic normality of the distribution function of sums of independent random variables that have finite variances. Let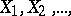 
be a sequence of independent random variables with means 
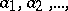and finite variances 
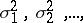not all of which are zero. Let
 |
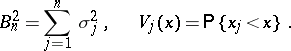In order that
 |
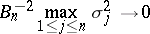and
 |
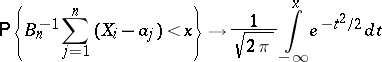for any 
as 
, it is necessary and sufficient that the following condition (the Lindeberg condition) is satisfied:
 |
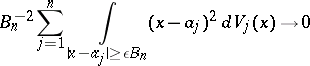as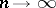 
for any 
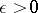. Sufficiency was proved by J.W. Lindeberg [1] and necessity by W. Feller [2].
References
| [1] | J.W. Lindeberg, "Eine neue Herleitung des Exponentialgesetzes in der Wahrscheinlichkeitsrechnung" Math. Z. , 15 (1922) pp. 211–225 |
| [2] | W. Feller, "Ueber den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung" Math. Z. , 40 (1935) pp. 521–559 |
| [3] | M. Loève, "Probability theory" , Springer (1977) |
| [4] | V.V. Petrov, "Sums of independent random variables" , Springer (1975) (Translated from Russian) |
How to Cite This Entry:
Lindeberg-Feller theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindeberg-Feller_theorem&oldid=22747
Lindeberg-Feller theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lindeberg-Feller_theorem&oldid=22747
This article was adapted from an original article by V.V. Petrov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article