Difference between revisions of "Lebesgue-Stieltjes integral"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Lebesgue–Stieltjes integral to Lebesgue-Stieltjes integral: ascii title) |
(No difference)
| |
Revision as of 18:53, 24 March 2012
A generalization of the Lebesgue integral. For a non-negative measure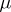 
the name "Lebesgue–Stieltjes integral" is used in the case when 
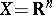and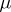 
is not the Lebesgue measure; then the integral 
is defined in the same way as the Lebesgue integral in the general case. If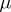 
is of variable sign, then 
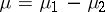, where 
and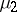 
are non-negative measures, and the Lebesgue–Stieltjes integral
 |
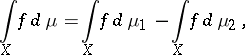under the condition that both integrals on the right-hand side exist. For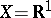 
the fact that 
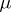is countably additive and bounded is equivalent to the fact that the measure is generated by some function 
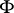of bounded variation. In this case the Lebesgue–Stieltjes integral is written in the form
 |
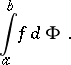For a discrete measure the Lebesgue–Stieltjes integral is a series of numbers.
References
| [1] | E. Kamke, "Das Lebesgue–Stieltjes-Integral" , Teubner (1960) |
Comments
References
| [a1] | E. Hewitt, K.R. Stromberg, "Real and abstract analysis" , Springer (1965) |
How to Cite This Entry:
Lebesgue-Stieltjes integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue-Stieltjes_integral&oldid=22717
Lebesgue-Stieltjes integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lebesgue-Stieltjes_integral&oldid=22717
This article was adapted from an original article by I.A. Vinogradova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article