Karush-Kuhn-Tucker conditions

KKT conditions, Karush–Kuhn–Tucker optimality conditions, KKT optimality conditions, Kuhn–Tucker conditions

Consider the general mathematical programming problem (see also Mathematical programming):

minimize , ,

subject to

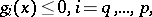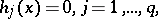with 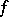, , 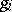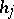all continuously differentiable, and form the Lagrangian function

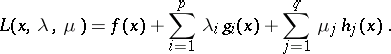The Karush–Kuhn–Tucker optimality conditions now are:

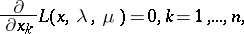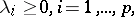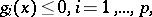Note that the two last conditions just say that is feasible and that the third conditions could be replaced by 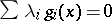(given the second and fourth). Under suitable constraint qualifications, the KKT optimality conditions are necessary conditions for a local solution 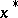of the general mathematical programming problem, in the following sense.

If 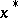is a local minimum, then there are corresponding 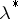, 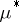such that the triple 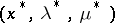satisfies the KKT optimality conditions. A triple satisfying the KKT optimality conditions is sometimes called a KKT-triple.

This generalizes the familiar Lagrange multipliers rule (see Lagrange multipliers) to the case where there are also inequality constraints.

The result was obtained independently by Karush in 1939, by F. John in 1948, and by H.W. Kuhn and J.W. Tucker in 1951, see [a1].

One suitable constraint qualification (for the case where there are no equality constraints) is 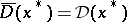, where 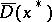is the closure of

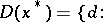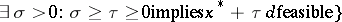and

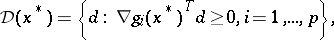where 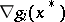is the gradient vector of 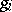at ,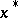

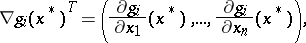[a2].

Given a KKT-triple 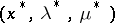, there are also (as in the case of Lagrange multipliers) second-order sufficient conditions that ensure local optimality of .

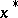References

[a1]	A.V. Fiacco, G.P. McCormick, "Nonlinear programming, sequential unconstrained minimization techniques" , SIAM (1968) (Edition: Reprinted)
[a2]	W.I. Zangwill, "Nonlinear programming" , Prentice-Hall (1969)
[a3]	O.L. Mangasarian, "Nonlinear programming" , McGraw-Hill (1969)
[a4]	G.P. McCormick, "Nonlinear programming: theory, algorithms, and applications" , Wiley (1983)
[a5]	Jong-Shi Pang, "Complementarity problems" R. Horst (ed.) P.M. Pardalos (ed.) , Handbook of Global Optimization , Kluwer Acad. Publ. (1995) pp. 271–338