Difference between revisions of "Hopf-Rinow theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Hopf–Rinow theorem to Hopf-Rinow theorem: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
If 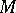 is a connected Riemannian space with distance function
is a connected Riemannian space with distance function 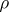 and a Levi-Civita connection, then the following assertions are equivalent:
and a Levi-Civita connection, then the following assertions are equivalent:
1)  is complete;
is complete;
2) for every point 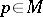 the exponential mapping
the exponential mapping 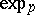 is defined on the whole tangent space
is defined on the whole tangent space 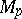 ;
;
3) every closed set  that is bounded with respect to
that is bounded with respect to  is compact.
is compact.
Corollary:
Any two points  can be joined in
can be joined in  by a geodesic of length
by a geodesic of length  . This was established by H. Hopf and W. Rinow [1].
. This was established by H. Hopf and W. Rinow [1].
A generalization of the Hopf–Rinow theorem (see [4]) is: If 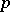 and
and  are two points in
are two points in 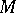 , then either there exists a curve joining them in a shortest way or there exists a geodesic
, then either there exists a curve joining them in a shortest way or there exists a geodesic 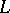 emanating from
emanating from  with the following properties: 1)
with the following properties: 1) 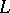 is homeomorphic to
is homeomorphic to 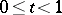 ; 2) if a sequence of points on
; 2) if a sequence of points on  does not have limit points on
does not have limit points on 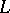 , then it does not have limit points in
, then it does not have limit points in 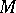 , that is,
, that is, 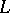 is closed in
is closed in 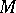 ; 3)
; 3)  contains the shortest connection between any two points on
contains the shortest connection between any two points on 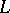 ; 4)
; 4) 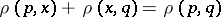 for every point
for every point 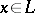 ; and 5) the length of
; and 5) the length of  is finite and does not exceed
is finite and does not exceed 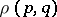 . Here the function
. Here the function  is not necessarily symmetric, and every point can be joined in a shortest possible (not necessarily unique) way to any point in a certain neighbourhood
is not necessarily symmetric, and every point can be joined in a shortest possible (not necessarily unique) way to any point in a certain neighbourhood  .
.
Corollary:
If there are no bounded rays in  , then every bounded set in
, then every bounded set in 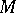 is compact.
is compact.
References
| [1] | H. Hopf, W. Rinow, "Ueber den Begriff der vollständigen differentialgeometrischen Flächen" Comm. Math. Helv. , 3 (1931) pp. 209–225 |
| [2] | G. de Rham, "Sur la réducibilité d'un espace de Riemann" Comm. Math. Helv. , 26 (1952) pp. 328–344 |
| [3] | D. Gromoll, W. Klingenberg, W. Meyer, "Riemannsche Geometrie im Grossen" , Springer (1968) |
| [4] | S.E. Cohn-Vossen, "Some problems of differential geometry in the large" , Moscow (1959) (In Russian) |
Comments
Let 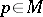 . The manifold
. The manifold  is called geodesically complete at
is called geodesically complete at 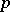 if
if 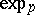 is defined on all of
is defined on all of 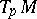 . The manifold
. The manifold 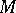 is geodesically complete if this holds for all
is geodesically complete if this holds for all 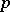 . The Hopf–Rinow theorem also includes the statement that geodesic completeness is equivalent to geodesic completeness at one
. The Hopf–Rinow theorem also includes the statement that geodesic completeness is equivalent to geodesic completeness at one  .
.
A geodesic joining  and
and 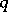 and of minimal length is called a minimizing geodesic.
and of minimal length is called a minimizing geodesic.
References
| [a1] | W. Klingenberg, "Riemannian geometry" , de Gruyter (1982) (Translated from German) |
Hopf-Rinow theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf-Rinow_theorem&oldid=22591