Difference between revisions of "Hausdorff-Young inequalities"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Hausdorff–Young inequalities to Hausdorff-Young inequalities: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
Estimates of the Fourier coefficients of functions in 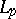 ; established by W.H. Young [1] and F. Hausdorff [2]. Let
; established by W.H. Young [1] and F. Hausdorff [2]. Let 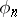 be an orthonormal system of functions on
be an orthonormal system of functions on 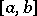 , let
, let 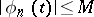 for all
for all 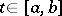 and for all
and for all 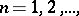 and let
and let 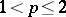 ,
, 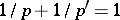 . If
. If 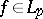 , then
, then
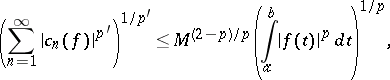 | (1) |
where 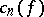 are the Fourier coefficients of
are the Fourier coefficients of 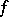 . If
. If 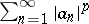 converges, there exists a function
converges, there exists a function 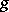 such that
such that
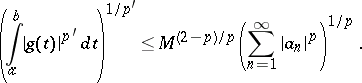 | (2) |
For 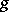 one may take
one may take 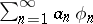 , and this series converges in
, and this series converges in 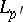 .
.
The Hausdorff–Young inequalities (1) and (2) are equivalent. For 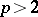 they do not hold. Moreover, if
they do not hold. Moreover, if 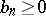 and if
and if 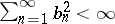 , then there exists a continuous function
, then there exists a continuous function 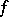 such that its Fourier coefficients
such that its Fourier coefficients 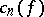 in the trigonometric system satisfy the condition
in the trigonometric system satisfy the condition 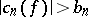 . A qualitative statement of the Hausdorff–Young inequality (if
. A qualitative statement of the Hausdorff–Young inequality (if 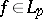 ,
, 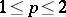 , then
, then 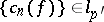 ) for unbounded orthonormal systems of functions does not hold, in general. An analogue of the Hausdorff–Young inequalities is valid for a broad class of function spaces.
) for unbounded orthonormal systems of functions does not hold, in general. An analogue of the Hausdorff–Young inequalities is valid for a broad class of function spaces.
References
| [1] | W.H. Young, "On the determination of the summability of a function by means of its Fourier constants" Proc. London Math. Soc. (2) , 12 (1913) pp. 71–88 |
| [2] | F. Hausdorff, "Eine Ausdehnung des Parsevalschen Satzes über Fourierreihen" Math. Z. , 16 (1923) pp. 163–169 |
| [3] | N.K. [N.K. Bari] Bary, "A treatise on trigonometric series" , Pergamon (1964) (Translated from Russian) |
| [4] | S. Kaczmarz, H. Steinhaus, "Theorie der Orthogonalreihen" , Chelsea, reprint (1951) |
| [5] | A. Zygmund, "Trigonometric series" , 2 , Cambridge Univ. Press (1988) |
| [6] | K. de Leeuw, J.P. Kahane, Y. Katznelson, "Sur les coefficients de Fourier des fonctions continues" C.R. Acad. Sci. Paris , 285 (1977) pp. 1001–1003 |
| [7] | S.G. Krein, Yu.I. Petunin, E.M. Semenov, "Interpolation of linear operators" , Amer. Math. Soc. (1982) (Translated from Russian) |
Comments
Taking for 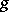 the series
the series 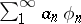 gives
gives 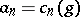 for all
for all 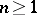 .
.
Hausdorff-Young inequalities. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hausdorff-Young_inequalities&oldid=22559