Difference between revisions of "Gauss-Manin connection"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Gauss–Manin connection to Gauss-Manin connection: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
The Gauss–Manin connection is a way to differentiate cohomology classes with respect to parameters. Consider a smooth projective curve  over a field
over a field  . Its first de Rham cohomology group
. Its first de Rham cohomology group  can be identified with the space of differentials of second kind on
can be identified with the space of differentials of second kind on  modulo exact differentials (cf. Differential). Each derivation
modulo exact differentials (cf. Differential). Each derivation  of
of  (cf. Derivation in a ring) can be lifted in a canonical way to a mapping
(cf. Derivation in a ring) can be lifted in a canonical way to a mapping  satisfying
satisfying  for
for  ,
,  [a1], [a2]. This amounts to a connection
[a1], [a2]. This amounts to a connection
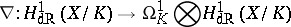 |
which is integrable (i.e.  ). If
). If  is a function field in one variable, one obtains the Picard–Fuchs equation
is a function field in one variable, one obtains the Picard–Fuchs equation  , which has regular singular points (cf. Regular singular point).
, which has regular singular points (cf. Regular singular point).
The generalization to higher dimension is due to A. Grothendieck [a3]. For a proper and smooth morphism  of
of 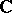 -schemes the de Rham cohomology of the fibres of
-schemes the de Rham cohomology of the fibres of  is described by the locally free
is described by the locally free  -modules
-modules  , the relative de Rham cohomology sheaves. From now on suppose that
, the relative de Rham cohomology sheaves. From now on suppose that  is of finite type over
is of finite type over 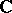 and let
and let  and
and  denote the underlying analytic spaces. Then
denote the underlying analytic spaces. Then
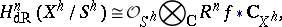 |
and the analytic version of the Gauss–Manin connection is defined by 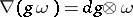 for
for  (respectively,
(respectively, 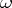 ) a local section of
) a local section of  (respectively,
(respectively,  ).
).
An algebraic construction has been given by N.M. Katz and T. Oda [a4]. The complex  is filtered by subcomplexes
is filtered by subcomplexes  , where
, where
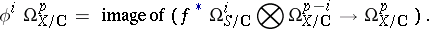 |
One has  and
and  . The connecting homomorphism
. The connecting homomorphism  in the long exact hypercohomology sequence associated to the exact sequence
in the long exact hypercohomology sequence associated to the exact sequence
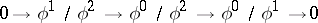 |
is an algebraic version of the Gauss–Manin connection.
The Gauss–Manin connection is regular singular [a5]–[a8]. Its monodromy transformations around points at infinity are quasi-unipotent [a6], [a9], [a10], and bounds on the size of its Jordan blocks are known [a7], [a11]. Geometrical proofs of the monodromy theorem are due to A. Landman [a12], C.H. Clemens [a13] and D.T. Lê [a14].
Another important feature of the Gauss–Manin connection is Griffiths' transversality. The relative de Rham cohomology sheaves of a smooth proper morphism  can be filtered as follows. Let
can be filtered as follows. Let 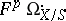 be the subcomplex
be the subcomplex
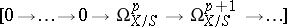 |
of 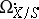 . Then
. Then  . The spectral sequence
. The spectral sequence  degenerates at
degenerates at  [a15] and
[a15] and  is locally free on
is locally free on 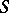 . Hence
. Hence 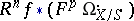 maps injectively to a subsheaf
maps injectively to a subsheaf  of
of  . Griffiths' transversality is the property that
. Griffiths' transversality is the property that
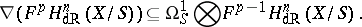 |
The geometric data  have given rise to the concept of a (polarized) variation of Hodge structure. A. Borel has extended the monodromy theorem to this abstract case ([a16], (6.1)).
have given rise to the concept of a (polarized) variation of Hodge structure. A. Borel has extended the monodromy theorem to this abstract case ([a16], (6.1)).
The Gauss–Manin connection has also been defined for function germs with isolated singularity [a10] and for mapping germs defining isolated complete intersection singularities [a17]. The monodromy of these connections is the classical Picard–Lefschetz monodromy on the vanishing cohomology.
In the theory of  -modules (cf.
-modules (cf.  -module), the theory of the Gauss–Manin connection is expressed as a property of the direct image functor for a proper morphism. Combined with the formalism of vanishing cycle functors [a18] it gives rise to the notion of the Gauss–Manin system [a19]. This plays an important role in the asymptotic Hodge theory of singularities [a20]–[a22].
-module), the theory of the Gauss–Manin connection is expressed as a property of the direct image functor for a proper morphism. Combined with the formalism of vanishing cycle functors [a18] it gives rise to the notion of the Gauss–Manin system [a19]. This plays an important role in the asymptotic Hodge theory of singularities [a20]–[a22].
References
| [a1] | Yu. Manin, "Algebraic curves over fields with differentiation" Transl. Amer. Math. Soc. , 37 (1964) pp. 59–78 Izv. Akad. Nauk. SSSR Ser. Mat. , 22 (1958) pp. 737–756 |
| [a2] | N.M. Katz, "On the differential equations satisfied by period matrices" Publ. Math. IHES , 35 (1968) pp. 71–106 |
| [a3] | A. Grothendieck, "On the de Rham cohomology of algebraic varieties" Publ. Math. IHES , 29 (1966) pp. 351–359 |
| [a4] | N.M. Katz, T. Oda, "On the differentiation of de Rham cohomology classes with respect to parameters" J. Math. Kyoto Univ. ,  (1968) pp. 199–213 (1968) pp. 199–213 |
| [a5] | N. Nilsson, "Some growth and ramification properties of certain integrals on algebraic manifolds" Arkiv för Mat. , 5 (1963–1965) pp. 527–540 |
| [a6] | P. Deligne, "Equations différentielles à points singuliers réguliers" , Lect. notes in math. , 163 , Springer (1970) |
| [a7] | N.M. Katz, "The regularity theorem in algebraic geometry" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 437–443 |
| [a8] | P.A. Griffiths, "Periods of integrals on algebraic manifolds, I, II" Amer. J. Math. , 90 (1968) pp. 568–626; 805–865 |
| [a9] | A. Grothendieck, "Letter to J.-P. Serre" (5.10.1964) |
| [a10] | E. Brieskorn, "Die Monodromie von isolierten Singularitäten von Hyperflächen" Manuscr. Math. , 2 (1970) pp. 103–161 |
| [a11] | N.M. Katz, "Nilpotent connections and the monodromy theorem. Applications of a result of Turrittin" Publ. Math. IHES , 39 (1971) pp. 175–232 |
| [a12] | A. Landman, "On the Picard–Lefschetz formula for algebraic manifolds acquiring general singularities" , Berkeley (1967) (Thesis) |
| [a13] | C.H. Clemens, "Picard–Lefschetz theorem for families of nonsingular algebraic varieties acquiring ordinary singularities" Trans. Amer. Math. Soc. , 136 (1969) pp. 93–108 |
| [a14] | D.T. Lê, "The geometry of the monodromy theorem" K.G. Ramanathan (ed.) , C.P. Ramanujam, a tribute , Tata IFR Studies in Math. , 8 , Springer (1978) |
| [a15] | P. Deligne, "Théorème de Lefschetz et critères de dégénérescence de suites spectrales" Publ. Math. IHES , 35 (1968) pp. 107–126 |
| [a16] | W. Schmid, "Variation of Hodge structure: the singularities of the period mapping" Invent. Math. , 22 (1973) pp. 211–319 |
| [a17] | G.-M. Greuel, "Der Gauss–Manin Zusammenhang isolierter Singularitäten von vollständigen Durchschnitten" Math. Ann. , 214 (1975) pp. 235–266 |
| [a18] | P. Deligne, "Le formalisme des cycles évanescents" A. Grothendieck (ed.) , Groupes de monodromie en géométrie algébrique. SGA 7.II , Lect. notes in math. , 340 , Springer (1973) pp. Exp. XIII |
| [a19] | F. Pham, "Singularités des systèmes différentiels de Gauss–Manin" , Birkhäuser (1979) |
| [a20] | J. Scherk, J.H.M. Steenbrink, "On the mixed Hodge structure on the cohomology of the Milnor fibre" Math. Ann. , 271 (1985) pp. 641–665 |
| [a21] | A.N. Varchenko, "Asymptotic Hodge structure in the vanishing cohomology" Math USSR Izv. , 18 (1982) pp. 469–512 Izv. Akad. Nauk SSSR , 45 : 3 (1981) pp. 540–591; 688 |
| [a22] | M. Saito, "Gauss–Manin system and mixed Hodge structure" Proc. Japan Acad. Ser A , 58 (1982) pp. 29–32 |
Gauss-Manin connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Gauss-Manin_connection&oldid=22497