Difference between revisions of "Gårding inequality"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Gårding inequality to Garding inequality: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
An inequality of the form
 |
where 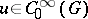 is a complex-valued function with compact support (in
is a complex-valued function with compact support (in 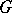 ),
),  is a bounded domain and
is a bounded domain and
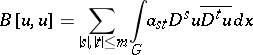 |
is a quadratic integral form with complex continuous coefficients 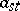 in
in 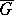 . A sufficient condition for the Gårding inequality to be valid for any function
. A sufficient condition for the Gårding inequality to be valid for any function 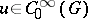 is the existence of a positive constant
is the existence of a positive constant  such that
such that
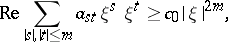 |
for any  and all real vectors
and all real vectors 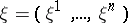 . Formulated and proved by L. Gårding [1].
. Formulated and proved by L. Gårding [1].
References
| [1] | L. Gårding, "Dirichlet's problem for linear elliptic partial differential equations" Math. Scand. , 1 (1953) pp. 55–72 |
| [2] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 |
Comments
A sharp form of this inequality has been given by L. Hörmander. See [a1], Sects. 18.1, 18.6, and the literature quoted there.
References
| [a1] | L.V. Hörmander, "The analysis of linear partial differential operators" , 3 , Springer (1985) |
How to Cite This Entry:
Gårding inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A5rding_inequality&oldid=22479
Gårding inequality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=G%C3%A5rding_inequality&oldid=22479
This article was adapted from an original article by A.A. Dezin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article