Revision as of 18:52, 24 March 2012
One of the numerical characteristics of a function of several variables that can be regarded as a multi-dimensional analogue of the variation of a function of a single variable. Suppose that a real-valued function  is given on the
is given on the  -dimensional parallelopipedon
-dimensional parallelopipedon
and introduce the notation
Let  be an arbitrary partition of
be an arbitrary partition of  by hyperplanes
by hyperplanes
into  -dimensional parallelopipeda, and let
-dimensional parallelopipeda, and let  take the values
take the values  in an arbitrary way. The Fréchet variation is defined as follows:
in an arbitrary way. The Fréchet variation is defined as follows:
If 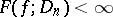 , then one says that
, then one says that  has bounded (finite) Fréchet variation on
has bounded (finite) Fréchet variation on  , and the class of all such functions is denoted by
, and the class of all such functions is denoted by  . For
. For  , this class was introduced by M. Fréchet [1] in connection with the investigation of the general form of a bilinear continuous functional
, this class was introduced by M. Fréchet [1] in connection with the investigation of the general form of a bilinear continuous functional  on the space of functions of the form
on the space of functions of the form  that are continuous on the square
that are continuous on the square  . He proved that every such functional can be represented in the form
. He proved that every such functional can be represented in the form
where  ,
,  .
.
Analogues of many of the classical criteria for the convergence of Fourier series are valid for 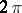 -periodic functions in the class
-periodic functions in the class  (
(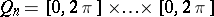 , see [2]). For example, if
, see [2]). For example, if  ,
,  then the rectangular partial sums of the Fourier series of
then the rectangular partial sums of the Fourier series of  converge at every point
converge at every point  to the number
to the number
where the summation is taken over all the 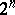 possible combinations of the signs
possible combinations of the signs  . Here, if the function is continuous, the convergence is uniform (an analogue of the Jordan criterion).
. Here, if the function is continuous, the convergence is uniform (an analogue of the Jordan criterion).
References
| [1] | M. Fréchet, "Sur les fonctionelles bilinéaires" Trans. Amer. Math. Soc. , 16 : 3 (1915) pp. 215–234 |
| [2] | M. Morse, W. Transue, "The Fréchet variation and the convergence of multiple Fourier series" Proc. Nat. Acad. Sci. USA , 35 : 7 (1949) pp. 395–399 |
How to Cite This Entry:
Fréchet variation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fr%C3%A9chet_variation&oldid=22465
This article was adapted from an original article by B.I. Golubov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article is given on the
is given on the  -dimensional parallelopipedon
-dimensional parallelopipedon
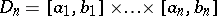
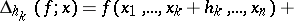
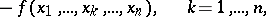
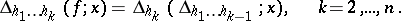
 be an arbitrary partition of
be an arbitrary partition of  by hyperplanes
by hyperplanes
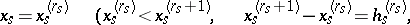
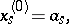
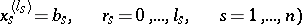
 -dimensional parallelopipeda, and let
-dimensional parallelopipeda, and let  take the values
take the values  in an arbitrary way. The Fréchet variation is defined as follows:
in an arbitrary way. The Fréchet variation is defined as follows:
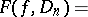
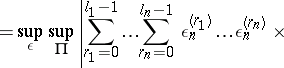
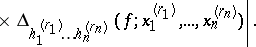
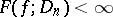 , then one says that
, then one says that  has bounded (finite) Fréchet variation on
has bounded (finite) Fréchet variation on  , and the class of all such functions is denoted by
, and the class of all such functions is denoted by  . For
. For  , this class was introduced by M. Fréchet [1] in connection with the investigation of the general form of a bilinear continuous functional
, this class was introduced by M. Fréchet [1] in connection with the investigation of the general form of a bilinear continuous functional  on the space of functions of the form
on the space of functions of the form  that are continuous on the square
that are continuous on the square  . He proved that every such functional can be represented in the form
. He proved that every such functional can be represented in the form
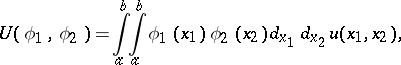
 ,
,  .
.
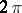 -periodic functions in the class
-periodic functions in the class  (
(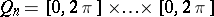 , see [2]). For example, if
, see [2]). For example, if  ,
,  then the rectangular partial sums of the Fourier series of
then the rectangular partial sums of the Fourier series of  converge at every point
converge at every point  to the number
to the number
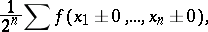
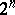 possible combinations of the signs
possible combinations of the signs  . Here, if the function is continuous, the convergence is uniform (an analogue of the Jordan criterion).
. Here, if the function is continuous, the convergence is uniform (an analogue of the Jordan criterion).