Difference between revisions of "Fourier-Stieltjes series"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Fourier–Stieltjes series to Fourier-Stieltjes series: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
A series
 |
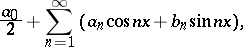where for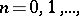 
 |
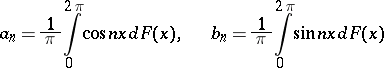(the integrals are taken in the sense of Stieltjes). Here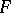 
is a function of bounded variation on 
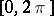. Alternatively one could write
 | (*) |
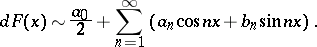If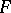 
is absolutely continuous on 
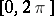, then (*) is the Fourier series of the function 
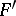. In complex form the series (*) is
 |
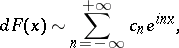where
 |
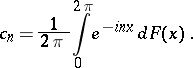Moreover,
 |
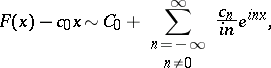and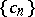 
will be bounded. If 
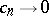, then 
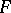is continuous on 
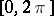. There is a continuous function 
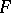for which 
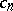does not tend to 
as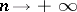 
. The series (*) is summable to 
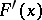by the Cesàro method 
, 
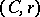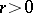, almost-everywhere on 
.
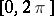References
| [1] | A. Zygmund, "Trigonometric series" , 1 , Cambridge Univ. Press (1988) |
How to Cite This Entry:
Fourier-Stieltjes series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier-Stieltjes_series&oldid=22447
Fourier-Stieltjes series. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier-Stieltjes_series&oldid=22447
This article was adapted from an original article by A.A. Konyushkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article