Difference between revisions of "Fourier-Bessel integral"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Fourier–Bessel integral to Fourier-Bessel integral: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
Hankel integral
An analogue of the Fourier integral for Bessel functions, having the form
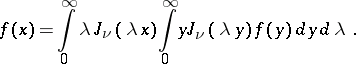 | (*) |
Formula (*) can be obtained from the Fourier–Bessel series for the interval 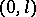 by taking the limit as
by taking the limit as 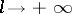 . H. Hankel (1875) established the following theorem: If the function
. H. Hankel (1875) established the following theorem: If the function 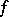 is piecewise continuous, has bounded variation on any interval
is piecewise continuous, has bounded variation on any interval 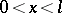 , and if the integral
, and if the integral
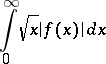 |
converges, then (*) is valid for 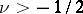 at all points where
at all points where 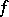 is continuous,
is continuous, 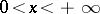 . At a point of discontinuity
. At a point of discontinuity 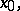
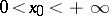 , the right-hand side of (*) is equal to
, the right-hand side of (*) is equal to 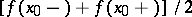 , and when
, and when  it gives
it gives 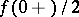 .
.
Analogues of the Fourier–Bessel integral (*) for other types of cylinder functions 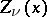 are also true, but the limits in the integrals should be changed accordingly.
are also true, but the limits in the integrals should be changed accordingly.
Comments
In case 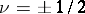 , formula (*) reduces to Fourier's sine and cosine integral, respectively. In case
, formula (*) reduces to Fourier's sine and cosine integral, respectively. In case 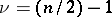 , where
, where 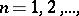 formula (*) can be interpreted as a Fourier integral for radial functions on
formula (*) can be interpreted as a Fourier integral for radial functions on 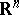 . See also [a1], p. 240.
. See also [a1], p. 240.
References
| [a1] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) |
Fourier-Bessel integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fourier-Bessel_integral&oldid=22437