Difference between revisions of "Fitzsimmons-Fristedt-Shepp theorem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (moved Fitzsimmons–Fristedt–Shepp theorem to Fitzsimmons-Fristedt-Shepp theorem: ascii title) |
(No difference)
| |
Revision as of 18:52, 24 March 2012
A theorem asserting that two particular random sets obtained in quite different ways have the same distribution law [a1]. A first version of this theorem was obtained by B. Mandelbrot in 1972 [a2]. It is a key fact for understanding the link between random coverings and potential theory (see also Dvoretzky problem; Billard method).
The first random set is defined as
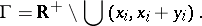 |
Here, the random cutouts  are associated with points
are associated with points  that are randomly distributed in
that are randomly distributed in  in such a way that their number in any given rectangle
in such a way that their number in any given rectangle  is a Poisson random variable (cf. Poisson process) with parameter
is a Poisson random variable (cf. Poisson process) with parameter  , where
, where  is the Lebesgue measure and
is the Lebesgue measure and  is a given measure on
is a given measure on  that is locally bounded except at
that is locally bounded except at  . The set of points
. The set of points  is called a point Poisson process with intensity
is called a point Poisson process with intensity  , and
, and  can be viewed as the set of points in
can be viewed as the set of points in  that are never in the shadow of the point Poisson process when light comes from the directions
that are never in the shadow of the point Poisson process when light comes from the directions 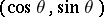 ,
, 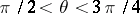 .
.
The second random set is the closure of the range of a positive Lévy process with drift  and Lévy measure
and Lévy measure  . By definition, this process,
. By definition, this process,  (
(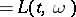 ), has independent and stationary increments, and
), has independent and stationary increments, and
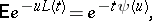 |
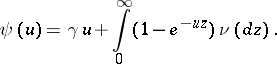 |
The theorem asserts that for any given 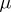 with
with
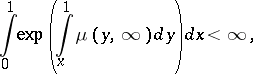 | (a1) |
one can explicitly define 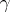 and
and  in such a way that
in such a way that
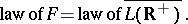 |
The drift  vanishes precisely when
vanishes precisely when
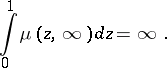 |
For example, when 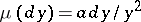 ,
,  , then
, then  and
and  (this is the case of a stable Lévy process of index
(this is the case of a stable Lévy process of index  ).
).
When the integral in (a1) is infinite, a formal computation gives  and
and  concentrated at
concentrated at  . This is the case when
. This is the case when 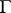 is empty. Therefore, the Fitzsimmons–Fristedt–Shepp theorem is an extension of Shepp's theorem, which states that (a1) is a necessary and sufficient condition for
is empty. Therefore, the Fitzsimmons–Fristedt–Shepp theorem is an extension of Shepp's theorem, which states that (a1) is a necessary and sufficient condition for  almost surely [a3].
almost surely [a3].
Now, given a compact subset  of
of  , the probabilities of the events
, the probabilities of the events  and
and  are the same; in other words:
are the same; in other words:  almost surely if and only if
almost surely if and only if  is a polar set for the Lévy process
is a polar set for the Lévy process  . Since compact polar sets are precisely the compact sets of vanishing capacity with respect to a potential kernel (associated with
. Since compact polar sets are precisely the compact sets of vanishing capacity with respect to a potential kernel (associated with  and
and  and therefore with
and therefore with 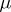 ), the link between Poisson covering of
), the link between Poisson covering of  and potential theory is manifest (see also Billard method).
and potential theory is manifest (see also Billard method).
References
| [a1] | P.J. Fitzsimons, B. Fristedt, L.R. Shepp, "The set of real numbers left uncovered by random covering intervals" Z. Wahrscheinlichkeitsth. verw. Gebiete , 70 (1985) pp. 175–189 |
| [a2] | B.B. Mandelbrot, "Renewal sets and random cutouts" Z. Wahrscheinlichkeitsth. verw. Gebiete , 22 (1972) pp. 145–157 |
| [a3] | L.A. Shepp, "Covering the line by random intervals" Z. Wahrscheinlichkeitsth. verw. Gebiete , 23 (1972) pp. 163–170 |
Fitzsimmons-Fristedt-Shepp theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Fitzsimmons-Fristedt-Shepp_theorem&oldid=22429